Advertisements
Advertisements
प्रश्न
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of the water required to fill the whole tube is `5159/6 cm^3` and `4235/6 cm^3` of water is required to fill the tube to a level which is 4 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.
उत्तर
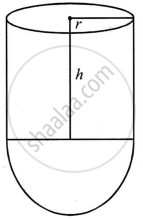
Volume of water filled in the test tube =`5159/6 cm^3`
Volume of water filled up to 4 cm =`4235/6 cm^3`
Let r be the radius and h be the height of test tube
∴ `2/3 pir^3 + pir^2h = 5159/6`
`=> pir^2(2/3r + h) = 5159/6`
`=> (pir^2)/3(2r + 3h) = 5159/6`
`=> pir^2(2r + 3h) = 5159/2` ...(i)
And
`2/3pir^3 + pir^2(h - 4) = 4235/6`
`=> pir^2(2/3r + h - 4) = 4235/6`
`=> (pir^2)/3(2r + 3h - 12) = 4235/6`
`=> pir^2(2r + 3h - 12) = 4235/2` ...(ii)
Dividing (i) by (ii)
`(2r + 3h)/(2r + 3h - 12) = 5259/4235` ...(iii)
Subtracting (ii) from (i)
`pir^2(12) = 5159/2 - 4235/2 = 924/2`
`=> 12 xx 22/7 xx r^2 = 924/2`
`=> r^2 = (924 xx 7)/(2 xx 12 xx 22) = (7 xx 7)/(2 xx 2)`
`=> r^2 = 49/4`
`=> r = 7/2 = 3.5 cm`
Subtracting the value of r in (iii)
`(2 xx 7/2 + 3h)/(2 xx 7/2 + 3h - 12) = 5159/4235`
`=> (7 + 3h)/(7 + 3h - 12) = 5159/4235`
`=> (7 + 3h)/(7 + 3h - 12) = 469/385`
`=>` 2695 + 1155h = 1407h – 2345
`=>` 252h = 5040
`=>` h = 20
Hence, height = 20 cm and radius = 3.5 cm
APPEARS IN
संबंधित प्रश्न
A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
`["Assume "pi=22/7]`
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gm of mass (approx). (Take π = `355/113`)
Water flows, at 9 km per hour, through a cylindrical pipe of cross-sectional area 25 cm2. If this water is collected into a rectangular cistern of dimensions 7.5 m by 5 m by 4 m; calculate the rise in level in the cistern in 1 hour 15 minutes.
How much iron is needed to make a rod of length 90 cm and diameter 1.4 cm?
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the internal volume of the container in m3.
The radius and height of a cylinder are in the ratio of 5 : 7 and its volume is 550 cm. Find its radius. (Take π = 22/7)
The diameter of the cross-section of a water pipe is 5 cm. Water flows through it at 10km/hr into a cistern in the form of a cylinder. If the radius of the base of the cistern is 2.5 m, find the height to which the water will rise in the cistern in 24 minutes.
A small village, having a population of 5000, requires 75 litres of water per head per day. The village has got an overhead tank of measurement 40 m × 25 m × 15 m. For how many days will the water of this tank last?
A cylindrical tube opened at both the ends is made of iron sheet which is 2 cm thick. If the outer diameter is 16 cm and its length is 100 cm, find how many cubic centimeters of iron has been used in making the tube?
