Advertisements
Advertisements
प्रश्न
A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
`["Assume "pi=22/7]`
उत्तर
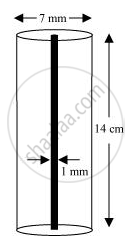
Radius (r1) of pencil = (7/2)mm = (0.7/2)cm = 0.35 cm
Radius (r2) of graphite = (1/2)mm = (0.1/2)cm = 0.05 cm
Height (h) of pencil = 14 cm
`"Volume of wood in pencil "=pi(r_1^2-r_2^2)h`
`=[22/7{(0.35)^2-(0.05)^2xx14}]cm^3`
`=[22/7(0.1225-0.0025)xx14]cm^3`
= (44 x 0.12) cm3
= 5.28 cm3
`"Volume of graphite "=pir_2^2h=[22/7xx(0.05)^2xx14]cm^3`
= (44 x 0.0025) cm3
= 0.11 cm3
APPEARS IN
संबंधित प्रश्न
A cylindrical boiler, 2 m high, is 3.5 m in diameter. It has a hemispherical lid. Find the volume of its interior, including the part covered by the lid.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m.
Calculate:
- the total area of the internal surface, excluding the base;
- the internal volume of the container in m3.
Find the total surface area of an open pipe of length 50 cm, external diameter 20 cm and internal diameter 6 cm.
Find the volume of the cylinder if the circumference of the cylinder is 132 cm and height is 25 cm.
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along its :
- shorter side.
- longer side.
The radius and height of a cylinder are in the ratio of 5 : 7 and its volume is 550 cm. Find its radius. (Take π = 22/7)
If the circumference of a conical wooden piece is 484 cm then find its volume when its height is 105 cm.
A sphere and a right circular cylinder of the same radius have equal volumes. By what percentage does the diameter of the cylinder exceed its height?
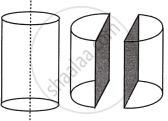
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.
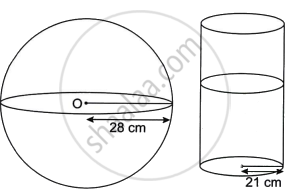
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`