Advertisements
Advertisements
प्रश्न
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gm of mass (approx). (Take π = `355/113`)
उत्तर
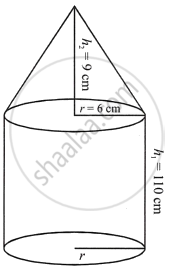
Radius of the base of poles (r) = 6 cm
Height of the cylindrical part (h1) = 110 cm
Height of the conical part (h2) = 9 cm
Total volume of the iron pole
= `pir^2h_1 + 1/3pir^2h_2`
= `pir^2(h_1 + 1/3h_2)`
= `355/113 xx 6 xx 6(110 + 1/3xx9)`
= `355/113 xx 36 xx 113`
= 12780 cm3
Weight of 1 cm3 = 8 gm
Therefore, total weight = 12780 × 8
= 102240 gm
= 102.240 kg ...`[∵ 1 gm = 1/1000 kg]`
= 102.24 kg
APPEARS IN
संबंधित प्रश्न
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
`["Assume "pi=22/7]`
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is `4 2/3` m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
A cylindrical boiler, 2 m high, is 3.5 m in diameter. It has a hemispherical lid. Find the volume of its interior, including the part covered by the lid.
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate:
- the total surface area of the can in contact with water when the sphere is in it;
- the depth of water in the can before the sphere was put into the can.
Two solid cylinders, one with diameter 60 cm and height 30 cm and the other with radius 30 cm and height 60 cm, are metled and recasted into a third solid cylinder of height 10 cm. Find the diameter of the cylinder formed.
A small village, having a population of 5000, requires 75 litres of water per head per day. The village has got an overhead tank of measurement 40 m × 25 m × 15 m. For how many days will the water of this tank last?
The volume of a cylinder which exactly fits in a cube of side a is ______.
From a pipe of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in 1 hour.
A rectangular sheet of paper is rolled in two different ways to form two different cylinders. Find the volume of cylinders in each case if the sheet measures 44 cm × 33 cm.
