Advertisements
Advertisements
Question
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gm of mass (approx). (Take π = `355/113`)
Solution
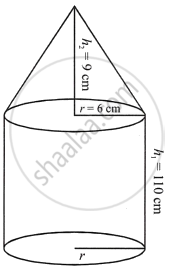
Radius of the base of poles (r) = 6 cm
Height of the cylindrical part (h1) = 110 cm
Height of the conical part (h2) = 9 cm
Total volume of the iron pole
= `pir^2h_1 + 1/3pir^2h_2`
= `pir^2(h_1 + 1/3h_2)`
= `355/113 xx 6 xx 6(110 + 1/3xx9)`
= `355/113 xx 36 xx 113`
= 12780 cm3
Weight of 1 cm3 = 8 gm
Therefore, total weight = 12780 × 8
= 102240 gm
= 102.240 kg ...`[∵ 1 gm = 1/1000 kg]`
= 102.24 kg
APPEARS IN
RELATED QUESTIONS
A soft drink is available in two packs − (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
`["Assume "pi=22/7]`
It costs Rs 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of Rs 20 per m2, find
(i) Inner curved surface area of the vessel
(ii) Radius of the base
(iii) Capacity of the vessel
`["Assume "pi=22/7]`
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base is removed. Find the volume of the remaining solid.
A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate :
- total surface area of the tent,
- area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.
Water flows, at 9 km per hour, through a cylindrical pipe of cross-sectional area 25 cm2. If this water is collected into a rectangular cistern of dimensions 7.5 m by 5 m by 4 m; calculate the rise in level in the cistern in 1 hour 15 minutes.
How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter ? Also, find the cost of plastering its inner surface at Rs 4.50 per sq meter.
The height of a circular cylinder is 20 cm and the radius of its base is 7 cm. Find :
- the volume
- the total surface area.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the total area of the internal surface, excluding the base.
A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)
Volume of a cylinder with radius h and height r is ______.
