Advertisements
Advertisements
Question
A soft drink is available in two packs − (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
`["Assume "pi=22/7]`
Solution
The tin can will be cuboidal in shape while the plastic cylinder will be cylindrical in shape.
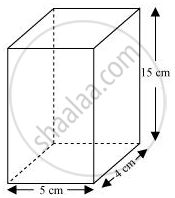
Length (l) of tin can = 5 cm
Breadth (b) of tin can = 4 cm
Height (h) of tin can = 15 cm
Capacity of tin can = l × b × h
= (5 × 4 × 15) cm3
= 300 cm3
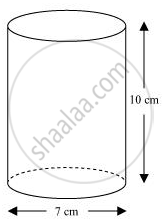
Radius (r) of circular end of plastic cylinder = (7/2)cm = 3.5 cm
Height (H) of plastic cylinder = 10 cm
Capacity of plastic cylinder = πr2H
`=[22/7xx(3.5)^2xx10]cm^3`
= (11 x 35) cm3
= 385 cm3
Therefore, plastic cylinder has the greater capacity.
Difference in capacity = (385 − 300) cm3 = 85 cm3
APPEARS IN
RELATED QUESTIONS
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find (i) radius of its base (ii) its volume. [Use π = 3.14]
A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
`["Assume "pi=22/7]`
Water flows, at 9 km per hour, through a cylindrical pipe of cross-sectional area 25 cm2. If this water is collected into a rectangular cistern of dimensions 7.5 m by 5 m by 4 m; calculate the rise in level in the cistern in 1 hour 15 minutes.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m.
Calculate:
- the total area of the internal surface, excluding the base;
- the internal volume of the container in m3.
A cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2 (sq. cm). Find the height of the cylinder correct to one decimal place.
Water is being pumped out through a circular pipe whose external diameter is 7 cm. If the flow of water is 72 cm per second how many litres of water are being pumped out in one hour.
Water flows through a cylindrical pipe of internal diameter 7 cm at 36 km/hr. Calculate the time in minutes it would take to fill the cylindrical tank, the radius of whose base is 35 cm, and height is 1 m.
A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass?
In a hollow cylinder, the sum of the external and internal radii is 14 cm and the width is 4 cm. If its height is 20 cm, the volume of the material in it is
A housing society consisting of 5,500 people needs 100 L of water per person per day. The cylindrical supply tank is 7 m high and has a diameter 10 m. For how many days will the water in the tank last for the society?
