Advertisements
Advertisements
Question
A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass?
Solution
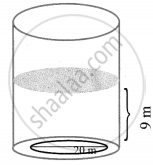
Radius of the cylindrical glass (r) = 10 cm
Height of the water (h) = 9 cm
Radius of the cylindrical metal (R) = 5 cm
Height of the metal (H) = 4 cm
Let the height of the water raised be h
Volume of the water raised in the cylinder = Volume of the cylindrical metal
πr2h = πr2H
π × 102 × h = π × 52 × 4
h = `100/100`
h = 1 cm
∴ The height of the raised water in the glass = 1 cm.
APPEARS IN
RELATED QUESTIONS
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find (i) radius of its base (ii) its volume. [Use π = 3.14]
A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
`["Assume "pi=22/7]`
The height of a circular cylinder is 20 cm and the radius of its base is 7 cm. Find :
- the volume
- the total surface area.
A circular tank of diameter 2 m is dug and the earth removed is spread uniformly all around the tank to form an embankment 2 m in width and 1.6 m in height. Find the depth of the circular tank.
A cylindrical vessel of height 24 cm and diameter 40 cm is full of water. Find the exact number of small cylindrical bottles, each of height 10 cm and diameter 8 cm, which can be filled with this water.
The diameter of the cross-section of a water pipe is 5 cm. Water flows through it at 10km/hr into a cistern in the form of a cylinder. If the radius of the base of the cistern is 2.5 m, find the height to which the water will rise in the cistern in 24 minutes.
The volume of a cylinder becomes ______ the original volume if its radius becomes half of the original radius.
The radius and height of a cylinder are in the ratio 3 : 2 and its volume is 19,404 cm3. Find its radius and height.
Radius of a cylinder is r and the height is h. Find the change in the volume if the height remains same and the radius is halved.
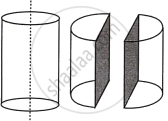
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.