Advertisements
Advertisements
Question
A circular tank of diameter 2 m is dug and the earth removed is spread uniformly all around the tank to form an embankment 2 m in width and 1.6 m in height. Find the depth of the circular tank.
Solution
Given, diameter of circular tank = 2 m
And width of embankment = 2 m
Height = 1.6 m

Radius of tank = `2/2` = 1 m
Outer radius of embankment = 1 + 2 = 3 m
∴ Volume of earth = π(R2 – r2) × h
= `22/7 (3^2 - 1^2) xx 1.6 m^3`
= `22/7 xx (9 - 1) xx 1.6 m^3`
= `22/7 xx 8 xx 1.6 m^3`
= `22/7 xx 12.8 m^3`
Now volume of the earth dug out from the tank
= `22/7 xx 12.8 m^3`
Radius of tank = 1 m
∴ Depth of circular
= `"Volume"/(pir^2)`
= `(22 xx 12.8 xx 7)/(7 xx 22 xx 1 xx 1)`
= 12.8 m
APPEARS IN
RELATED QUESTIONS
The circumference of the base of the cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1000 cm3 = 1l)
`["Assume "pi=22/7]`
Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
- To find how much it can hold
- Number of cement bags required to plaster it
- To find the number of smaller tanks that can be filled with water from it.
Water flows, at 9 km per hour, through a cylindrical pipe of cross-sectional area 25 cm2. If this water is collected into a rectangular cistern of imensions 7.5 m by 5 m by 4 m; calculate therise in level in the cistern in 1 hour 15 minutes.

Calculate:
(a) the total surface area,
(b) the total volume of the solid and
(c) the density of the material if its total weight is 1.7 kg..
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m.
Calculate:
- the total area of the internal surface, excluding the base;
- the internal volume of the container in m3.
A cylinderical container with a diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimesions 22 cm × 14 cm × 10.5 cm. Find the rise in level of the water when the solid is submerged.
If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
The radii of two cylinders are in the ratio of 2:3 and their heights are in the ratio of 5:3. The ratio of their volumes is ______.
The volume of a cylinder which exactly fits in a cube of side a is ______.
Two cylinders A and B are formed by folding a rectangular sheet of dimensions 20 cm × 10 cm along its length and also along its breadth respectively. Then volume of A is ______ of volume of B.
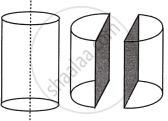
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.