Advertisements
Advertisements
Question
A cylinderical container with a diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimesions 22 cm × 14 cm × 10.5 cm. Find the rise in level of the water when the solid is submerged.
Solution
Given:
cylindrical container
D = 42 cm
r = `42/2 = 21` cm
H = ?
Rectangular solid
l = 22
b = 14
h = 10.5 cm
The volume of container = The volume of solid
πr2H = l × b × h
`22/7 xx 21 xx 21 xx "H" = 22 xx 14 xx 10.5`
`"H" = (22 xx 14 xx 10.5 xx 7)/(22 xx 21 xx 21)`
= `(2 xx 10.5)/9`
= `21/9`
= `7/3`
H = `2 1/3` or 2.33 cm
APPEARS IN
RELATED QUESTIONS
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
`["Assume "pi=22/7]`
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid.
Find the volume of the cylinder if the circumference of the cylinder is 132 cm and height is 25 cm.
The total surface area of a solid cylinder is 616 cm2. If the ratio between its curved surface area and total surface area is 1 : 2; find the volume of the cylinder.
A glass cylinder with a diameter 20 cm water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which water will rise in the cylinder. (Take π = 3.142)
A sphere and a right circular cylinder of the same radius have equal volumes. By what percentage does the diameter of the cylinder exceed its height?
Volume of a cylinder with radius h and height r is ______.
A hollow garden roller of 42 cm diameter and length 152 cm is made of cast iron 2 cm thick. Find the volume of iron used in the roller.
Volume of a cylinder is 330 cm3. The volume of the cone having same radius and height as that of the given cylinder is:
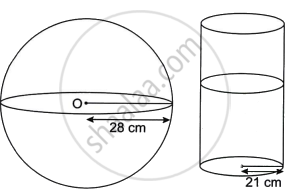
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`