Advertisements
Advertisements
Question
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid.
Solution
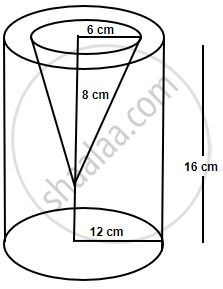
Radius of solid cylinder (R) = 12 cm
and Height (H) = 16 cm
∴ Volume = πR2H
= `22/7 xx 12 xx 12 xx 16`
= `50688/7 cm^3`
Radius of cone (r) = 6 cm and height (h) = 8 cm.
∴ Volume = `1/3pir^2h`
= `1/3 xx 22/7 xx 6 xx 6 xx 8`
= `2112/7 cm^3`
(i) Volume of remaining solid
= `50688/7-2112/7`
= `48567/7`
= 6939.43 cm3
(ii) Slant height of cone `l = sqrt(h^2 + r^2)`
= `sqrt(6^2 + 8^2)`
= `sqrt(36 + 64)`
= `sqrt(100)`
= 10 cm
Therefore, total surface area of remaining solid = curved surface area of cylinder + curved surface area of cone + base area of cylinder + area of circular ring on upper side of cylinder
= `2piRH + pirl + piR^2 + pi(R^2 - r^2)`
= `(2 xx 22/7 xx 12 xx 16) + (22/7 xx 6 xx 10) + (22/7 xx 12 xx 12) + (22/7(12^2 - 6^2))`
= `8448/7 + 1320/7 + 3168/7 + 22/7(144 - 36)`
= `8448/7 + 1320/7 + 3168/7 + 2376/7`
= `15312/7`
= 2187.43 cm2
APPEARS IN
RELATED QUESTIONS
A soft drink is available in two packs − (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
`["Assume "pi=22/7]`
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find (i) radius of its base (ii) its volume. [Use π = 3.14]
It costs Rs 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of Rs 20 per m2, find
(i) Inner curved surface area of the vessel
(ii) Radius of the base
(iii) Capacity of the vessel
`["Assume "pi=22/7]`
A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 m s–1. Calculate, in minutes, the time it takes to fill the tank.
What length of solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of external diameter 20 cm, 0.25 cm thickand 15 cm long?
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is 1 : 2 : 3.
A sphere and a right circular cylinder of the same radius have equal volumes. By what percentage does the diameter of the cylinder exceed its height?
30 circular plates, each of radius 14 cm and thickness 3 cm are placed one above the another to form a cylindrical solid. Find volume of the cylinder so formed.
If the height of a cylinder becomes `1/4` of the original height and the radius is doubled, then which of the following will be true?
The radius and height of a cylinder are in the ratio 3 : 2 and its volume is 19,404 cm3. Find its radius and height.
