Advertisements
Advertisements
प्रश्न
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid.
उत्तर
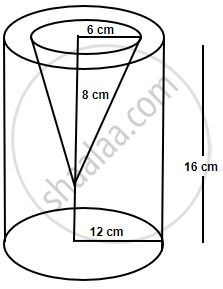
Radius of solid cylinder (R) = 12 cm
and Height (H) = 16 cm
∴ Volume = πR2H
= `22/7 xx 12 xx 12 xx 16`
= `50688/7 cm^3`
Radius of cone (r) = 6 cm and height (h) = 8 cm.
∴ Volume = `1/3pir^2h`
= `1/3 xx 22/7 xx 6 xx 6 xx 8`
= `2112/7 cm^3`
(i) Volume of remaining solid
= `50688/7-2112/7`
= `48567/7`
= 6939.43 cm3
(ii) Slant height of cone `l = sqrt(h^2 + r^2)`
= `sqrt(6^2 + 8^2)`
= `sqrt(36 + 64)`
= `sqrt(100)`
= 10 cm
Therefore, total surface area of remaining solid = curved surface area of cylinder + curved surface area of cone + base area of cylinder + area of circular ring on upper side of cylinder
= `2piRH + pirl + piR^2 + pi(R^2 - r^2)`
= `(2 xx 22/7 xx 12 xx 16) + (22/7 xx 6 xx 10) + (22/7 xx 12 xx 12) + (22/7(12^2 - 6^2))`
= `8448/7 + 1320/7 + 3168/7 + 22/7(144 - 36)`
= `8448/7 + 1320/7 + 3168/7 + 2376/7`
= `15312/7`
= 2187.43 cm2
APPEARS IN
संबंधित प्रश्न
A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 m s–1. Calculate, in minutes, the time it takes to fill the tank.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m.
Calculate:
- the total area of the internal surface, excluding the base;
- the internal volume of the container in m3.
How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter? Also, find the cost of plastering its inner surface at Rs. 4.50 per sq.meter.
A cylindrical container with internal radius of its base 10 cm, contains water up to a height of 7 cm. Find the area of the wet surface of the cylinder.
The height and the radius of the base of a cylinder are in the ratio 3 : 1. If it volume is 1029 π cm3; find it total surface area.
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along it : longer side.
A glass cylinder with a diameter 20 cm water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which water will rise in the cylinder. (Take π = 3.142)
A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass?
The barrel of a fountain-pen cylindrical in shape is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen will be used for writing 330 words on an average. How many words can be written using a bottle of ink containing one-fifth of a litre?
A school provides milk to the students daily in a cylindrical glasses of diameter 7 cm. If the glass is filled with milk upto an height of 12 cm, find how many litres of milk is needed to serve 1600 students.
