Advertisements
Advertisements
प्रश्न
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 80 m, calculate the total area of canvas required. Also, find the total cost of canvas used at Rs. 15 per metre if the width is 1.5 m.
उत्तर
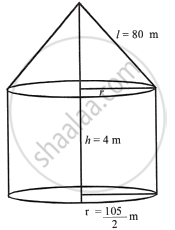
Radius of the cylindrical part of the tent (r) = `105/2 m`
Slant height (l) = 80 m
Therefore, total curved surface area of the tent = 2πrh + πrl
= `(2 xx 22/7 xx 105/2 xx 4) + (22/7 xx 105/2 xx 80)`
= 1320 + 13200
= 14520 m2
Width of canvas used = 1.5 m
Length of canvas = `14520/1.5 = 9680 m`
Total cost of canvas at the rate of Rs. 15 per meter
= 9680 × 15
= Rs. 145200
APPEARS IN
संबंधित प्रश्न
It costs Rs 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of Rs 20 per m2, find
(i) Inner curved surface area of the vessel
(ii) Radius of the base
(iii) Capacity of the vessel
`["Assume "pi=22/7]`
Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
- To find how much it can hold
- Number of cement bags required to plaster it
- To find the number of smaller tanks that can be filled with water from it.
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is `3 1/2` cm and height 8 cm. Find the volume of water required to fill the vessel. If this cone is replaced by another cone, whose height is `1 3/4` cm and the radius of whose base is 2 cm, find the drop in the water level.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m.
Calculate:
- the total area of the internal surface, excluding the base;
- the internal volume of the container in m3.
A cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2 (sq. cm). Find the volume of the cylinder correct to one decimal place.
Water is being pumped out through a circular pipe whose external diameter is 7 cm. If the flow of water is 72 cm per second how many litres of water are being pumped out in one hour.
If the height of a cylinder becomes `1/4` of the original height and the radius is doubled, then which of the following will be true?
Two cylinders of equal volume have heights in the ratio 1 : 9. The ratio of their radii is ______.
Two cylinders of same volume have their radii in the ratio 1 : 6, then ratio of their heights is ______.
Radius of a cylinder is r and the height is h. Find the change in the volume if the height is doubled and the radius is halved.
