Advertisements
Advertisements
प्रश्न
Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
- To find how much it can hold
- Number of cement bags required to plaster it
- To find the number of smaller tanks that can be filled with water from it.
उत्तर
- We must determine the cylindrical tank's volume in order to determine how much a cylinder can contain.
- We must determine the cylindrical tank's surface area in order to determine how many cement bags will be needed to plaster the tank.
- We must calculate the volumes of the big cylindrical tank and one tiny tank in order to determine which smaller tanks can be filled with water from the larger tank.
APPEARS IN
संबंधित प्रश्न
Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?

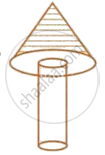
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of the water required to fill the whole tube is `5159/6 cm^3` and `4235/6 cm^3` of water is required to fill the tube to a level which is 4 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.
The inner radius of a pipe is 2.1 cm. How much water can 12 m of this pipe hold?
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for `4 1/2` seconds at the rate of 9 complete rounds per second. Find the distance travelled by the cylinder in `4 1/2` seconds.
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for `4 1/2` seconds at the rate of 9 complete rounds per second. Find the area covered by the cylinder in `4 1/2` seconds.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the total area of the internal surface, excluding the base.
A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass?
Metallic discs of radius 0.75 cm and thickness 0.2 cm are melted to obtain 508.68 cm3 of metal. Find the number of discs melted (use π = 3.14).
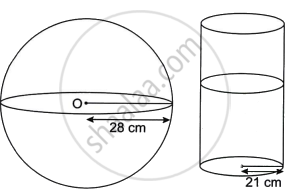
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`