Advertisements
Advertisements
प्रश्न
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid.
उत्तर
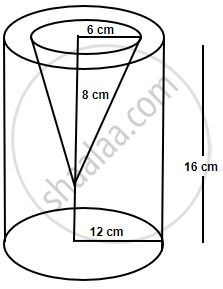
Radius of solid cylinder (R) = 12 cm
and Height (H) = 16 cm
∴ Volume = πR2H
= `22/7 xx 12 xx 12 xx 16`
= `50688/7 cm^3`
Radius of cone (r) = 6 cm and height (h) = 8 cm.
∴ Volume = `1/3pir^2h`
= `1/3 xx 22/7 xx 6 xx 6 xx 8`
= `2112/7 cm^3`
(i) Volume of remaining solid
= `50688/7-2112/7`
= `48567/7`
= 6939.43 cm3
(ii) Slant height of cone `l = sqrt(h^2 + r^2)`
= `sqrt(6^2 + 8^2)`
= `sqrt(36 + 64)`
= `sqrt(100)`
= 10 cm
Therefore, total surface area of remaining solid = curved surface area of cylinder + curved surface area of cone + base area of cylinder + area of circular ring on upper side of cylinder
= `2piRH + pirl + piR^2 + pi(R^2 - r^2)`
= `(2 xx 22/7 xx 12 xx 16) + (22/7 xx 6 xx 10) + (22/7 xx 12 xx 12) + (22/7(12^2 - 6^2))`
= `8448/7 + 1320/7 + 3168/7 + 22/7(144 - 36)`
= `8448/7 + 1320/7 + 3168/7 + 2376/7`
= `15312/7`
= 2187.43 cm2
APPEARS IN
संबंधित प्रश्न
Find the volume of the cylinder if the height (h) and radius of the base (r) are as given below.
r = 10.5 cm, h = 8 cm
Find the volume of the cylinder if the circumference of the cylinder is 132 cm and height is 25 cm.
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm3 of the metal weights 7.7 g.
The difference between the outer curved surface area and the inner curved surface area of a hollow cylinder is 352 cm2. If its height is 28 cm and the volume of material in it is 704 cm3; find its external curved surface area.
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2 : 3. Find the ratio between their curved surface areas.
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2 : 3. Find the ratio between their volumes.
A closed cylindrical tank, made of thin ironsheet, has diameter = 8.4 m and height 5.4 m. How much metal sheet, to the nearest m2, is used in making this tank, if `1/15` of the sheet actually used was wasted in making the tank?
A glass cylinder with a diameter 20 cm water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which water will rise in the cylinder. (Take π = 3.142)
The radius of two right circular cylinder are in the ratio of 2 : 3 and their heights are in the ratio of 5: 4 calculate the ratio of their curved surface areas and also the ratio of their volumes.
A small village, having a population of 5000, requires 75 litres of water per head per day. The village has got an overhead tank of measurement 40 m × 25 m × 15 m. For how many days will the water of this tank last?
