Advertisements
Advertisements
Question
Volume of a cylinder is 330 cm3. The volume of the cone having same radius and height as that of the given cylinder is:
Options
330 cm3
165 cm3
110 cm3
220 cm3
Solution
110 cm3
Explanation:
Volume of a cylinder is 330 cm3.
Volume of a cylinder = πr2h
Volume of the cone = `1/3 πr^2h`
Volume of the cone = `1/3` × Volume of a cylinder
Volume of the cone = `1/3` × 330 cm3
Volume of the cone = 110 cm3
APPEARS IN
RELATED QUESTIONS
A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm × 14 cm × 10.5 cm. Find the rise in the level of the water when the solid is submerged.
What length of solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of external diameter 20 cm, 0.25 cm thickand 15 cm long?
A cylindrical container with internal radius of its base 10 cm, contains water up to a height of 7 cm. Find the area of the wet surface of the cylinder.
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along its :
- shorter side.
- longer side.
Two solid cylinders, one with diameter 60 cm and height 30 cm and the other with radius 30 cm and height 60 cm, are metled and recasted into a third solid cylinder of height 10 cm. Find the diameter of the cylinder formed.
A rectangular paper of width 14 cm is rolled along its width and a cylinder of radius 20 cm is formed. Find the volume of the cylinder. (Take `22/7` for π)

If the radius of a cylinder is doubled and height is halved, the volume will be doubled.
Two cylinders A and B are formed by folding a rectangular sheet of dimensions 20 cm × 10 cm along its length and also along its breadth respectively. Then volume of A is ______ of volume of B.
The radius and height of a cylinder are in the ratio 3 : 2 and its volume is 19,404 cm3. Find its radius and height.
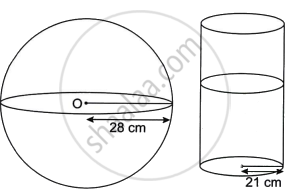
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`