Advertisements
Advertisements
प्रश्न
A circular tank of diameter 2 m is dug and the earth removed is spread uniformly all around the tank to form an embankment 2 m in width and 1.6 m in height. Find the depth of the circular tank.
उत्तर
Given, diameter of circular tank = 2 m
And width of embankment = 2 m
Height = 1.6 m

Radius of tank = `2/2` = 1 m
Outer radius of embankment = 1 + 2 = 3 m
∴ Volume of earth = π(R2 – r2) × h
= `22/7 (3^2 - 1^2) xx 1.6 m^3`
= `22/7 xx (9 - 1) xx 1.6 m^3`
= `22/7 xx 8 xx 1.6 m^3`
= `22/7 xx 12.8 m^3`
Now volume of the earth dug out from the tank
= `22/7 xx 12.8 m^3`
Radius of tank = 1 m
∴ Depth of circular
= `"Volume"/(pir^2)`
= `(22 xx 12.8 xx 7)/(7 xx 22 xx 1 xx 1)`
= 12.8 m
APPEARS IN
संबंधित प्रश्न
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid.
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate:
- the total surface area of the can in contact with water when the sphere is in it;
- the depth of water in the can before the sphere was put into the can.
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of the water required to fill the whole tube is `5159/6 cm^3` and `4235/6 cm^3` of water is required to fill the tube to a level which is 4 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.
How much water will a tank hold if the interior diameter of the tank is 1.6 m and its depth is 0.7 m?
The height of a circular cylinder is 20 cm and the radius of its base is 7 cm. Find : the total surface area.
Water flows through a cylindrical pipe of internal diameter 7 cm at 36 km/hr. Calculate the time in minutes it would take to fill the cylindrical tank, the radius of whose base is 35 cm, and height is 1 m.
The ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height is
The water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank contains 50 kilolitres of water. Water is pumped into the tank to fill to its capacity. Calculate the volume of water pumped into the tank.
A housing society consisting of 5,500 people needs 100 L of water per person per day. The cylindrical supply tank is 7 m high and has a diameter 10 m. For how many days will the water in the tank last for the society?
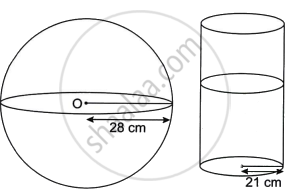
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`