Advertisements
Advertisements
प्रश्न
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate:
- the total surface area of the can in contact with water when the sphere is in it;
- the depth of water in the can before the sphere was put into the can.
उत्तर
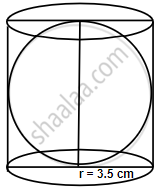
Radius of the base of the cylindrical can = 3.5 cm
i. When the sphere is in can, then total surface area of the can = Base area + Curved surface area
= `pir^2 + 2pirh`
= `(22/7 xx 3.5 xx 3.5) + (2 xx 22/7 xx 3.5 xx 7)`
= `77/2+154`
= 38.5 + 154
= 192.5 cm2
ii. Let depth of water = x cm
When sphere is not in the can, then volume of the can = Volume of water + Volume of sphere
`=> pir^2h + pir^2x xx + 4/3pir^3`
`=> pir^2h + pir^2(x + 4/3r)`
`=> h = x + 4/3r`
`=> x = h - 4/3r`
`=> x = 7 - 4/3 xx 7/2`
`=> x = 7 - 14/3`
`=> x = (21 - 14)/3`
`=> x = 7/3`
`=> x = 2 1/3 cm`
APPEARS IN
संबंधित प्रश्न
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is `4 2/3` m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 m s–1. Calculate, in minutes, the time it takes to fill the tank.
The height and the radius of the base of a cylinder are in the ratio 3 : 1. If it volume is 1029 π cm3; find it total surface area.
Find the volume of the cylinder if the height (h) and radius of the base (r) are as given below.
r = 10.5 cm, h = 8 cm
How much iron is needed to make a rod of length 90 cm and diameter 1.4 cm?
The total surface area of a solid cylinder is 616 cm2. If the ratio between its curved surface area and total surface area is 1 : 2; find the volume of the cylinder.
The radius of two right circular cylinder are in the ratio of 2 : 3 and their heights are in the ratio of 5: 4 calculate the ratio of their curved surface areas and also the ratio of their volumes.
A 14 m deep well with inner diameter 10 m is dug and the earth taken out is evenly spread all around the well to form an embankment of width 5 m. Find the height of the embankment.
The volume of a cylinder becomes ______ the original volume if its radius becomes half of the original radius.
A rectangular sheet of paper is rolled in two different ways to form two different cylinders. Find the volume of cylinders in each case if the sheet measures 44 cm × 33 cm.
