Advertisements
Advertisements
प्रश्न
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate:
- the total surface area of the can in contact with water when the sphere is in it;
- the depth of water in the can before the sphere was put into the can.
उत्तर
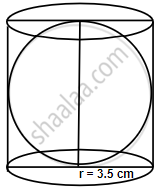
Radius of the base of the cylindrical can = 3.5 cm
i. When the sphere is in can, then total surface area of the can = Base area + Curved surface area
= `pir^2 + 2pirh`
= `(22/7 xx 3.5 xx 3.5) + (2 xx 22/7 xx 3.5 xx 7)`
= `77/2+154`
= 38.5 + 154
= 192.5 cm2
ii. Let depth of water = x cm
When sphere is not in the can, then volume of the can = Volume of water + Volume of sphere
`=> pir^2h + pir^2x xx + 4/3pir^3`
`=> pir^2h + pir^2(x + 4/3r)`
`=> h = x + 4/3r`
`=> x = h - 4/3r`
`=> x = 7 - 4/3 xx 7/2`
`=> x = 7 - 14/3`
`=> x = (21 - 14)/3`
`=> x = 7/3`
`=> x = 2 1/3 cm`
APPEARS IN
संबंधित प्रश्न
It costs Rs 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of Rs 20 per m2, find
(i) Inner curved surface area of the vessel
(ii) Radius of the base
(iii) Capacity of the vessel
`["Assume "pi=22/7]`
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m.
Calculate:
- the total area of the internal surface, excluding the base;
- the internal volume of the container in m3.
A cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2 (sq. cm). Find the height of the cylinder correct to one decimal place.
A cylindrical container with internal radius of its base 10 cm, contains water up to a height of 7 cm. Find the area of the wet surface of the cylinder.
The total surface area of a cone whose radius is `r/2` and slant height 2l is ______.
The radii of two cylinders are in the ratio of 2:3 and their heights are in the ratio of 5:3. The ratio of their volumes is ______.
A school provides milk to the students daily in a cylindrical glasses of diameter 7 cm. If the glass is filled with milk upto an height of 12 cm, find how many litres of milk is needed to serve 1600 students.
Radius of a cylinder is r and the height is h. Find the change in the volume if the height is doubled and the radius is halved.
Volume of a cylinder of height 3 cm is a 48π. Radius of the cylinder is ______.
