Advertisements
Advertisements
प्रश्न
A soft drink is available in two packs − (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
`["Assume "pi=22/7]`
उत्तर
The tin can will be cuboidal in shape while the plastic cylinder will be cylindrical in shape.
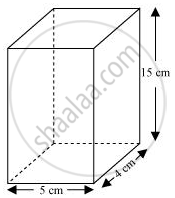
Length (l) of tin can = 5 cm
Breadth (b) of tin can = 4 cm
Height (h) of tin can = 15 cm
Capacity of tin can = l × b × h
= (5 × 4 × 15) cm3
= 300 cm3
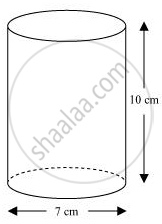
Radius (r) of circular end of plastic cylinder = (7/2)cm = 3.5 cm
Height (H) of plastic cylinder = 10 cm
Capacity of plastic cylinder = πr2H
`=[22/7xx(3.5)^2xx10]cm^3`
= (11 x 35) cm3
= 385 cm3
Therefore, plastic cylinder has the greater capacity.
Difference in capacity = (385 − 300) cm3 = 85 cm3
APPEARS IN
संबंधित प्रश्न
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base is removed. Find the volume of the remaining solid.
A cylindrical boiler, 2 m high, is 3.5 m in diameter. It has a hemispherical lid. Find the volume of its interior, including the part covered by the lid.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m.
Calculate:
- the total area of the internal surface, excluding the base;
- the internal volume of the container in m3.
A cylindrical container with internal radius of its base 10 cm, contains water up to a height of 7 cm. Find the area of the wet surface of the cylinder.
A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)
A 14 m deep well with inner diameter 10 m is dug and the earth taken out is evenly spread all around the well to form an embankment of width 5 m. Find the height of the embankment.
In a hollow cylinder, the sum of the external and internal radii is 14 cm and the width is 4 cm. If its height is 20 cm, the volume of the material in it is
Two cylinders of equal volume have heights in the ratio 1 : 9. The ratio of their radii is ______.
How many cubic metres of earth must be dug to construct a well 7 m deep and of diameter 2.8 m?
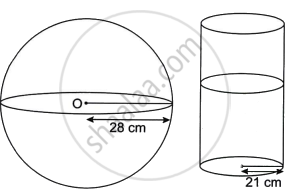
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`