Advertisements
Advertisements
प्रश्न
A solid is in the form of a right circular cone mounted on a hemisphere. The diameter of the base of the cone, which exactly coincides with hemisphere, is 7 cm and its height is 8 cm. The solid is placed in a cylindrical vessel of internal radius 7 cm and height 10 cm. How much water, in cm3, will be required to fill the vessel completely?
उत्तर
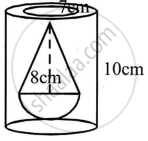
Diameter of hemisphere = 7 cm
Diameter of the base of the cone = 7 cm
Therefore, radius (r) = 3.5 cm
Height (h) = 8 cm
Volume of the solid = `1/3pir^2h + 2/3pir^3`
= `1/3pir^2(h + 2r)`
= `1/3 xx 22/7 xx 3.5 xx 3.5(8 + 2 xx 3.5)`
= `77/6(8 + 7)`
= `385/2`
= 192.5 cm3
Now, radius of cylindrical vessel (R) = 7 cm
Height (H) = 10 cm
∴ Volume = πR2h
= `22/7 xx 7 xx 7 xx 10`
= 1540 cm3
Volume of water required to fill
= 1540 – 192.5
= 1347.5 cm3
APPEARS IN
संबंधित प्रश्न
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
`["Assume "pi=22/7]`
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find
- radius of the base and
- total surface area of the cone.
`["Assume "pi =22/7]`
Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
Find the curved surface area of a cone with base radius 5.25 cm and slant height 10cm.
The radius and slant height of a cone are In the ratio of 4 : 7. If its curved surface area is 792 cm2, find its radius. (Use it 𝜋 = 22/7).
A Joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
The radius and height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the slant height and radius of the cone. (Use it 𝜋 = 3.14).
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilo litres?
The curved surface area of a cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find :
- the surface area of remaining solid,
- the volume of remaining solid,
- the weight of the material drilled out if it weighs 7 gm per cm3.
Find the curved surface area of a cone whose height is 8 cm and base diameter is 12 cm .
The radius and height of a cylinder, a cone and a sphere are same. Calculate the ratio of their volumes.
The surface area of a solid sphere is increased by 21% without changing its shape. Find the percentage increase in its: volume
The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm3. What is its radius? What is its slant height? (Take π = 3.14)
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
