Advertisements
Advertisements
प्रश्न
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
उत्तर
Height of solid cone (h) = 8 cm
Radius (r) = 6 cm
Volume of solid cone =
=
= 96π cm3
Height of smaller cone = 2 cm
And radius =
Volume of smaller cone
=
=
Number of cones so formed
=
=
= 576
APPEARS IN
संबंधित प्रश्न
Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
The radius of a cone is 7 cm and area of curved surface is 176
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Find the volume of a right circular cone with:
radius 3.5 cm, height 12 cm
The radius and the height of a right circular cone are in the ratio 5 : 12. If its volume is 314 cubic meter, find the slant height and the radius (Use it 𝜋 = 3.14).
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
Find the volume of the largest right circular cone that can be fitted in a cube whose edge is 14 cm.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilo litres?
The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2.
Calculate:
- its radius in cm.
- its volume in cm3. [Take π = 3.14].
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find :
- the surface area of remaining solid,
- the volume of remaining solid,
- the weight of the material drilled out if it weighs 7 gm per cm3.
A cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm, are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
The radii of the bases of two solid right circular cones of same height are r1 and r2 respectively. The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms r1, r2 and R.
A solid metallic hemisphere of diameter 28 cm is melted and recast into a number of identical solid cones, each of diameter 14 cm and height 8 cm. Find the number of cones so formed.
A sphere and a cone have the same radii. If their volumes are also equal, prove that the height of the cone is twice its radius.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2. Calculate: its volume in cm3. Take π = 3.14
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: height of the tent.
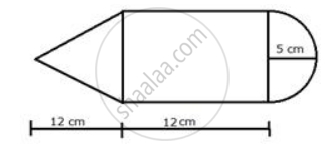
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg