Advertisements
Advertisements
प्रश्न
A cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
उत्तर
The diameter of the largest hemisphere that can be placed on a face of a cube of side 7 cm will be 7 cm.
Therefore, radius = r = `7/2` cm
Its curved surface area = 2πr2
= `2 xx 22/7 xx 7/2 xx 7/2`
= 77 cm2 ...(i)
Surface area of the top of the resulting solid = Surface area of the top face of the cube − Area of the base of the hemisphere
= `(7 xx 7) - (22/7 xx 49/4)`
= `49 - 77/2`
= `(98 - 77)/2`
= `21/2`
= 10.5 cm2 ...(ii)
Surface area of the cube = 5 × (side)2
= 5 × 49
= 245 cm2 ...(iii)
Total area of resulting solid = 245 + 10.5 + 77 = 332.5 cm2
APPEARS IN
संबंधित प्रश्न
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m
wide to make the required tent.
A bus stop is barricated from the remaining part of the road, by using 50 hollow cones made of recycled card-board. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is Rs. 12 per m2, what will be the cost of painting all these cones. (Use 𝜋 = 3.14 and √1.04 = 1.02)
The radius and the height of a right circular cone are in the ratio 5 : 12. If its volume is 314 cubic meter, find the slant height and the radius (Use it 𝜋 = 3.14).
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilo litres?
The internal and external diameter of a hollow hemispherical vessel are 21 cm and 28 cm respectively. Find :
- internal curved surface area,
- external curved surface area,
- total surface area,
- volume of material of the vessel.
The radii of the bases of two solid right circular cones of same height are r1 and r2 respectively. The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms r1, r2 and R.
A cone and a hemisphere have the same base and the same height. Find the ratio between their volumes.
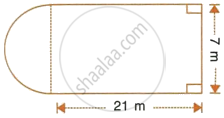
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
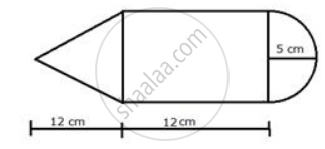
A solid, consisting of a right circular cone standing one a hemisphere, is placed upright in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of
the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimeter.
Curved surface area of a cone is 251.2 cm2 and radius of its base is 8 cm. Find its slant height and perpendicular height. (π = 3.14)
Total surface area of a cone is 616 sq.cm. If the slant height of the cone is three times the radius of its base, find its slant height.
Find the volume of the right circular cone whose height is 12 cm and slant length is 15 cm . (π = 3.14)
The curved surface area of a right circular cone of radius 11.3 cm is 710 cm2. What is the slant height of the cone ?
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the total volume of the solid.
The ratio of the base area and the curved surface of a conical tent is 40: 41. If the height is 18 m, Find the air capacity of the tent in terms of n.
The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm3. What is its radius? What is its slant height? (Take π = 3.14)
Water flows at the rate of 10 m per minute through a cylindrical pipe 5 mm of diameter. How much time would it take to fill a conical vessel whose diameter at he surface is 40 cm and depth is 24 cm?
