Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The radius and the height of a right circular cone are in the ratio 5 : 12. If its volume is 314 cubic meter, find the slant height and the radius (Use it ЁЭЬЛ = 3.14).
рдЙрддреНрддрд░
Let the ratio be x
∴ Radius `r`= 5x
Height ‘h’ = 12x
WKT,
∴ Slant height`= sqrt(r^2+h^2)=sqrt((5x)^2+(12x)^2)=13x`
Now volume`=314m^3` [given data]
⇒`1/3pir^2h=314m^3 `
⇒`1/3xx3.14xx25x^2xx12x=314`
⇒`x^3=(314xx3)/(3.14xx25xx12)`
⇒`x^3=1⇒x=1`
∴ Slant height = 13x=13m
Radius=5x=5m
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
The radius of a cone is 7 cm and area of curved surface is 176 `cm^2`. Find the slant height.
The area of the curved surface of a cone is 60яБ░ cm2. If the slant height of the cone be 8 cm, find the radius of the base?
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs. 210 per l00 m2.
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
Two right circular cone x and y are made x having three times the radius of y and y having half the volume of x. Calculate the ratio between the heights of x and y.
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is Rs.10 per sq.m? `(π = 22/7)`
Volume of a cone is 1232 cm3 and its height is 24 cm. Find the surface area of the cone. `( π = 22/7)`
Total surface area of a cone is 616 sq.cm. If the slant height of the cone is three times the radius of its base, find its slant height.
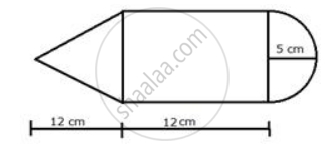
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg
