Advertisements
Advertisements
Question
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones used.
Solution
Let the number of cones melted be n.
Let the radius of sphere be rs = 6 cm
Radius of cone be rc = 2 cm
And height of the cone be h = 3 cm
Volume of sphere = n ...(Volume of a metallic cone)
`=> 4/3 pir_s^3 = n(1/3 pir_c^2h)`
`=> 4/3 pir_s^3 = n(1/3 pir_c^2h)`
`=> (4r_s^3)/(r_c^2h) = n`
`=> n = (4(6)^3)/((2)^2(3))`
`=> n = (4 xx 216)/(4 xx 3)`
`=>` n = 72
Hence, the number of cones is 72.
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of diameter 3.5 m.
`["Assume "pi=22/7]`
Find the radius of a sphere whose surface area is 154 cm2.
`["Assume "pi=22/7]`
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
- the radius of the sphere.
- the number of cones recast. (Take π = `22/7`)
Find the surface area of a sphere of radius 14 cm.
Find the surface area of a sphere of diameter 14 cm .
Find the surface area of a sphere of diameter 21 cm .
How many balls each of radius 1 cm can be made by melting a bigger ball whose diameter is 8 cm?
The volume of one sphere is 27 times that of another sphere. Calculate the ratio of their :
- radii,
- surface areas.
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the adjoining figure. The tunnel is 80 m long.
Calculate:
- its volume,
- the surface area of the tunnel (excluding the floor) and
- its floor area.

A cylindrical rod whose height is 8 times of its radius is melted and recast into spherical balls of same radius. The number of balls will be
If a solid sphere of radius 10 cm is moulded into 8 spherical solid balls of equal radius, then the surface area of each ball (in sq.cm) is
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
9 cm
The internal and external diameters of a hollow hemi-spherical vessel are 21 cm and 28 cm respectively. Find volume of material of the vessel.
The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate: the number of cones recasted [π = 3.14]
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
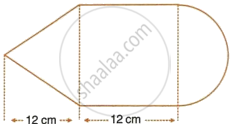
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
There is a ratio 1: 4 between the surface area of two spheres, find the ratio between their radius.
