Advertisements
Advertisements
Question
The radii of the internal and external surfaces of a metallic spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid right circular cone of height 32 cm. Find the diameter of the base of the cone.
Solution
Internal radius = 3 cm
External radius = 5 cm
Volume of spherical shell
= `4/3pi(5^3 - 3^3)`
= `4/3 xx 22/7(125 - 27)`
= `4/3 xx 22/7 xx 98`
Volume of solid circular cone
= `1/3pir^2h`
= `1/3 xx 22/7 xx r^2 xx 32`
Vol. of cone = Vol. of sphere
`=> 1/3 xx 22/7 xx r^2 xx 32 = 4/3 xx 22/7 xx 98`
`=> r^2 = (4 xx 98)/32`
∴ `r = 2 xx 7/2`
∴ r = 7 cm
APPEARS IN
RELATED QUESTIONS
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
`["Assume "pi=22/7]`
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹ 210 per 100 m2.
`["Assume "pi=22/7]`
Find the volume of a right circular cone with:
radius 3.5 cm, height 12 cm
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilo litres?
A solid metal sphere is cut through its center into 2 equal parts. If the diameter of the sphere is `3 1/2 cm`, find the total surface area of each part correct to two decimal places.
A buoy is made in the form of hemisphere surmounted by a right cone whose circular base coincides with the plane surface of hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-third of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find :
- the surface area of remaining solid,
- the volume of remaining solid,
- the weight of the material drilled out if it weighs 7 gm per cm3.
A solid is in the form of a right circular cone mounted on a hemisphere. The diameter of the base of the cone, which exactly coincides with hemisphere, is 7 cm and its height is 8 cm. The solid is placed in a cylindrical vessel of internal radius 7 cm and height 10 cm. How much water, in cm3, will be required to fill the vessel completely?
Find the radius of the circular base of the cone , if its volume is 154 cm3 and the perpendicular height is 12 cm
The heights of two cones are in the ratio 1:3 and their base radii are in the ratio 3:1. Find the ratio of their volumes.
The curved surface area of a right circular cone of radius 11.3 cm is 710 cm2. What is the slant height of the cone ?
The radius and height of a cylinder, a cone and a sphere are same. Calculate the ratio of their volumes.
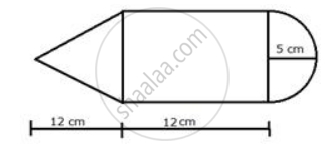
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg
The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm3. What is its radius? What is its slant height? (Take π = 3.14)
The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)
A conical tent is accommodate to 11 persons each person must have 4 sq. metre of the space on the ground and 20 cubic metre of air to breath. Find the height of the cone.
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. How many students can sit in the tent if a student, on an average, occupies `5/7` m2 on the ground?
