Advertisements
Advertisements
Question
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. How many students can sit in the tent if a student, on an average, occupies `5/7` m2 on the ground?
Solution
Given: Radius of the base of a conical tent = 5 cm
Area needs to sit a student on the ground = `5/7` m2
So, area of the base of a conical tent = `pir^2`
= `22/7 xx 5 xx 5 m^2`
Now, number of students = `"Area of the base of a conical tent"/"Area needs to sit a student on the ground"`
= `((22 xx 5 xx 5)/7)/(5/7)`
= `22/7 xx 5 xx 5 xx 7/5`
= 110
Hence, 110 students can sit in the conical tent.
APPEARS IN
RELATED QUESTIONS
The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface.
The curved surface area of a cone is 4070 cm2 and its diameter is 70 cm. What is its slant height? (Use it 𝜋 = 22/7).
There are two cones. The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8:5, show that the radius of each is to the height of each as 3:4.
If the radius of the base of a cone is halved, keeping the height same, what is the ratio of the volume of the reduced cone to that of the original cone?
The internal and external diameter of a hollow hemispherical vessel are 21 cm and 28 cm respectively. Find :
- internal curved surface area,
- external curved surface area,
- total surface area,
- volume of material of the vessel.
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone if it is completely filled.
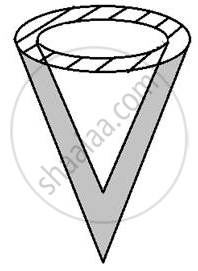
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
A hollow metallic cylindrical tube has an internal radius of 3.5 cm and height 21 cm. The thickness of the metal tube is 0.5 cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone, correct to one decimal place.
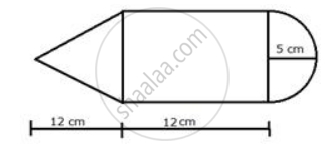
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg