Advertisements
Advertisements
Question
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8:5, show that the radius of each is to the height of each as 3:4.
Solution
Let us assume radius of cone=r.
Also, radius of cylinder=r.
And, height of cylinder=h.
Let` C_1` , be the curved surface area of cone
`∴ C_1=pirsqrt(r^2+h^2)`
Similarly,` C_2` be the curved surface area of cone cylinder.
`∴ C_2=2pirh`
According to question `C_2/C_1=8/5`
⇒ `(2pirh)/(pirsqrt(r^2+h^2))=8/5`
⇒ `10h=8sqrt(r^2+h^2)`
⇒ `100h^2=64r^2+64h^2`
⇒ `36h^2=64r^2`
`h/r=sqrt64/30`
⇒`(h/r)^2=64/36`
⇒` b/r=sqrt64/30=8/6=4/3`
`∴ r/h=3/4`
APPEARS IN
RELATED QUESTIONS
A joker’s cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
`["Assume "pi=22/7]`
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone.
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
Two right circular cone x and y are made x having three times the radius of y and y having half the volume of x. Calculate the ratio between the heights of x and y.
A heap of wheat is in the form of a cone of diameter 16.8 m and height 3.5 m. Find its volume. How much cloth is required to just cover the heap?
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the:
- radius of the floor,
- height of the tent,
- length of the canvas required to cover this conical tent if its width is 2 m.
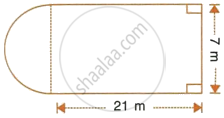
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
Curved surface area of a cone is 251.2 cm2 and radius of its base is 8 cm. Find its slant height and perpendicular height. (π = 3.14)
Find the cost of painting a hemispherical dome of diameter 10 m at the rate of Rs 1.40 per square metre.
The ratio of the base area and the curved surface of a conical tent is 40: 41. If the height is 18 m, Find the air capacity of the tent in terms of n.
