Advertisements
Advertisements
Question
A semi-circular sheet of metal of diameter 28 cm is bent to form an open conical cup. Find the capacity of the cup.
Solution
Given, diameter of a semi-circular sheet = 28 cm
∴ Radius of a semi-circular sheet, r = `28/2` = 14 cm
Since, a semi-circular sheet of metal is bent to form an open conical cup.
Let the radius of a conical cup be R.
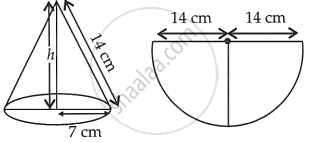
∴ Circumference base of cone = Circumference of semi-circle
2πR = πr
⇒ 2πR = π × 14
⇒ R = 7 cm
Now, `h = sqrt(l^2 - R^2)` ...[∵ l2 = h2 + R2]
= `sqrt(14^2 - 7^2)`
= `sqrt(196 - 49)`
= `sqrt(147)`
= 12.1243 cm
Volume (capacity) of conical cup = `1/3 piR^2h`
= `1/3 xx 22/7 xx 7 xx 7 xx 12.1243`
= 622.38 cm3
Hence, the capacity of an open conical cup is 622.38 cm3.
APPEARS IN
RELATED QUESTIONS
Find the volume of the right circular cone with radius 6 cm and height 7 cm.
`["Assume "pi=22/7]`
Find the capacity in litres of a conical vessel with radius 7 cm and slant height 25 cm.
`["Assume "pi=22/7]`
Find the capacity in litres of a conical vessel with height 12 cm and slant height 13 cm.
`["Assume "pi=22/7]`
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
`["Assume "pi=22/7]`
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find
- height of the cone
- slant height of the cone
- curved surface area of the cone
`["Assume "pi=22/7]`
Find the area of canvas required for a conical tent of height 24 m and base radius 7 m.
If the heights of two cones are in the ratio of 1 : 4 and the radii of their bases are in the ratio 4 : 1, then the ratio of their volumes is
If a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, the axis, the ratio of the volumes of upper and lower part is
If the ratio of radius of base and height of a cone is 5:12 and its volume is 314 cubic metre. Find its perpendicular height and slant height. (π = 3.14)
In a right circular cone, height, radius and slant height do not always be sides of a right triangle.
