Advertisements
Advertisements
Question
A cylindrical tube opened at both the ends is made of iron sheet which is 2 cm thick. If the outer diameter is 16 cm and its length is 100 cm, find how many cubic centimeters of iron has been used in making the tube?
Solution
According to the question,
Outer diameter d = 16 cm
Then, outer radius r = `16/2` = 8 cm
Height = Length = 100 cm
Thickness of iron sheet = 2 cm
Volume of cylinder = πr2h, where r = outer radius and π = 3.14
Thus, Volume of cylinder = πr2h
= 3.14 × (8)2 × 100
= 20,096 cm3
Now, inner diameter = outer diameter – 2 × thickness of iron sheet
Inner diameter = 16 – (2 × 2) = 12 cm
Inner radius R = `12/2` = 6 cm
Thus, Volume of hollow space = πR2 h, where R = inner radius and π = 3.14
= πR2h
= 3.14 × (6)2 × 100
= 11,304 cm3
Thus, Volume of iron used = Volume of cylinder – Volume of hollow space
= (20,096 – 11,304) cm3
= 8800 cm3
APPEARS IN
RELATED QUESTIONS
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gm of mass (approx). (Take π = `355/113`)
A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 m s–1. Calculate, in minutes, the time it takes to fill the tank.
What length of solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of external diameter 20 cm, 0.25 cm thick and 15 cm long?
A cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2 (sq. cm). Find the height of the cylinder correct to one decimal place.
Find the total surface area of an open pipe of length 50 cm, external diameter 20 cm and internal diameter 6 cm.
Find the volume of the cylinder if the height (h) and radius of the base (r) are as given below.
r = 10.5 cm, h = 8 cm
A circular tank of diameter 2 m is dug and the earth removed is spread uniformly all around the tank to form an embankment 2 m in width and 1.6 m in height. Find the depth of the circular tank.
Water is being pumped out through a circular pipe whose external diameter is 7 cm. If the flow of water is 72 cm per second how many litres of water are being pumped out in one hour.
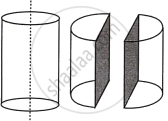
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.
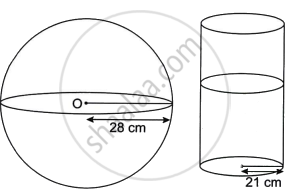
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`