Advertisements
Advertisements
प्रश्न
A semi-circular sheet of metal of diameter 28 cm is bent to form an open conical cup. Find the capacity of the cup.
उत्तर
Given, diameter of a semi-circular sheet = 28 cm
∴ Radius of a semi-circular sheet, r = `28/2` = 14 cm
Since, a semi-circular sheet of metal is bent to form an open conical cup.
Let the radius of a conical cup be R.
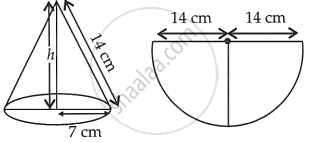
∴ Circumference base of cone = Circumference of semi-circle
2πR = πr
⇒ 2πR = π × 14
⇒ R = 7 cm
Now, `h = sqrt(l^2 - R^2)` ...[∵ l2 = h2 + R2]
= `sqrt(14^2 - 7^2)`
= `sqrt(196 - 49)`
= `sqrt(147)`
= 12.1243 cm
Volume (capacity) of conical cup = `1/3 piR^2h`
= `1/3 xx 22/7 xx 7 xx 7 xx 12.1243`
= 622.38 cm3
Hence, the capacity of an open conical cup is 622.38 cm3.
APPEARS IN
संबंधित प्रश्न
Find the volume of the right circular cone with radius 3.5 cm and height 12 cm.
`["Assume "pi=22/7]`
The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of its base. [Use π = 3.14]
The height of a cone is 15 cm. If its volume is 500 π cm3, then find the radius of its base.
If the volume of a right circular cone of height 9 cm is 48 `pi` cm3, find the diameter of its base.
If the height and slant height of a cone are 21 cm and 28 cm respectively. Find its volume.
A right circular cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is
Find the volume of a cone, if its total surface area is 7128 sq. cm and radius of base is 28 cm. `(π = 22/7)`
Volume of a cone is 6280 cubic cm and base radius of the cone is 20 cm. Find its perpendicular height. (π = 3.14)
There are 25 persons in a tent which is conical in shape. Every person needs an area of 4 sq.m. of the ground inside the tent. If height of the tent is 18 m, find the volume of the tent.
If the ratio of radius of base and height of a cone is 5:12 and its volume is 314 cubic metre. Find its perpendicular height and slant height. (π = 3.14)
