Advertisements
Advertisements
प्रश्न
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. How many students can sit in the tent if a student, on an average, occupies `5/7` m2 on the ground?
उत्तर
Given: Radius of the base of a conical tent = 5 cm
Area needs to sit a student on the ground = `5/7` m2
So, area of the base of a conical tent = `pir^2`
= `22/7 xx 5 xx 5 m^2`
Now, number of students = `"Area of the base of a conical tent"/"Area needs to sit a student on the ground"`
= `((22 xx 5 xx 5)/7)/(5/7)`
= `22/7 xx 5 xx 5 xx 7/5`
= 110
Hence, 110 students can sit in the conical tent.
APPEARS IN
संबंधित प्रश्न
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
A Joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Two cones have their heights in the ratio 1 : 3 and the radii of their bases in the ratio 3 : 1. Find the ratio of their volumes.
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
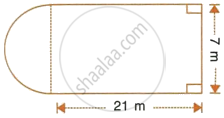
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is Rs.10 per sq.m? `(π = 22/7)`
A right-angled triangle PQR where ∠Q = 90° is rotated about QR and PQ. If QR = 16 cm and PR = 20 cm, compare the curved surface areas of the right circular cones so formed by the triangle
The ratio of the radii of two right circular cones of the same height is 1 : 3. Find the ratio of their curved surface area when the height cone is 3 times the radius of the smaller cone.
