Advertisements
Advertisements
Question
Find the volume of a right circular cone with:
radius 3.5 cm, height 12 cm
Solution
Given,
Radius of cone (r) =3.5cm
Height of cone (h)= 12cm
Volume of cone=`1/3pir^2h=1/3xx22/7xx(3.5)^2xx12`
`=154cm^3`
APPEARS IN
RELATED QUESTIONS
A conical tent is 10 m high and the radius of its base is 24 m. Find
- slant height of the tent.
- cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹ 70.
`["Assume "pi=22/7]`
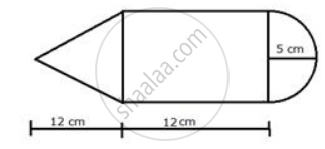
The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. This common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.

The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surfaces.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
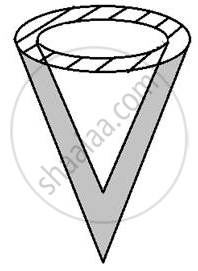
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
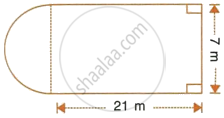
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
A solid, consisting of a right circular cone standing one a hemisphere, is placed upright in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of
the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimeter.
The heights of two cones are in the ratio 1:3 and their base radii are in the ratio 3:1. Find the ratio of their volumes.
The surface area of a solid sphere is increased by 21% without changing its shape. Find the percentage increase in its: volume
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the total volume of the solid.