Advertisements
Advertisements
Question
The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm3. What is its radius? What is its slant height? (Take π = 3.14)
Solution
Let the radius of cone be 3x cm and the height 4x cm, then
Volume of cone = `1/3`πr2h
⇒ `1/3` π (3x)2 (4x) = 301.44
⇒ x3 = 8
⇒ x = 2
Thus, radius of cone is 6 cm and height 8 cm.
Now,
slant height of cone = `sqrt( (6)^2 + (8)^2)` = 10 cm.
APPEARS IN
RELATED QUESTIONS
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
`["Assume "pi=22/7]`
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
`["Assume "pi=22/7]`
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹ 210 per 100 m2.
`["Assume "pi=22/7]`
A joker’s cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
`["Assume "pi=22/7]`
Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assume that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm (Use it 𝜋 = 3.14)
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
The curved surface area of a cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
A buoy is made in the form of hemisphere surmounted by a right cone whose circular base coincides with the plane surface of hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-third of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
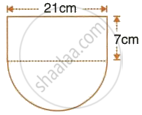
The given figure shows the cross section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: height of the tent.
The internal and external diameters of a hollow hemi-spherical vessel are 21 cm and 28 cm respectively. Find: external curved surface area .
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg
The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)
A metallic cylinder has a radius of 3 cm and a height of 5 cm. It is made of metal A. To reduce its weight, a conical hole is drilled in the cylinder, as shown and it is completely filled with a lighter metal B. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of the metal A to the volume of metal B in the solid.
How many square metres of canvas is required for a conical tent whose height is 3.5 m and the radius of the base is 12 m?
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. How many students can sit in the tent if a student, on an average, occupies `5/7` m2 on the ground?
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. Find the volume of the cone.
