Advertisements
Advertisements
Question
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
`["Assume "pi=22/7]`
Solution
Radius (r) of the base of cone = `(10.5/2) cm` = 5.25 cm
Slant height (l) of cone = 10 cm
∴ The curved surface area of the cone = πrl
= `(22/7 xx 5.25 xx 10) cm^2`
= `(22 xx 0.75 xx 10) cm^2`
= 165 cm2
Therefore, the curved surface area of the cone is 165 cm2.
APPEARS IN
RELATED QUESTIONS
Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
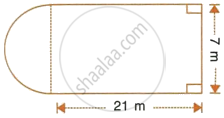
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
Volume of a cone is 1232 cm3 and its height is 24 cm. Find the surface area of the cone. `( π = 22/7)`
A hollow metallic cylindrical tube has an internal radius of 3.5 cm and height 21 cm. The thickness of the metal tube is 0.5 cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone, correct to one decimal place.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2. Calculate: its volume in cm3. Take π = 3.14
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: length of the canvas required to cover this conical tent if its width is 2 m.
A conical tent is accommodate to 11 persons each person must have 4 sq. metre of the space on the ground and 20 cubic metre of air to breath. Find the height of the cone.
