Advertisements
Advertisements
Question
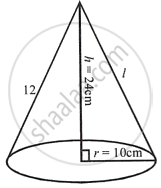
The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
Solution
The ratio between radius and height = 5 : 12
Volume = 2512 cubic cm
Let radius (r) = 5x, height (h) = 12x and slant height = l
l2 = r2 + h2
`=>` l2 = (5x)2 + (12x)2
`=>` l2 = 25x2 + 144x2
`=>` l2 = 169x2
`=>` l = 13x
Now volume = `1/3pir^2h`
`=> 1/3pir^2h = 2512`
`=> 1/3(3.14)(5x)^2(12x) = 2512`
`=> 1/3(3.14)(300x^3) = 2512`
∴ `x^3 = (2512 xx 3)/(3.14 xx 300)`
= `(2512 xx 3 xx 100)/(314 xx 300)`
= 8
`=>` x = 2
∴ Radius = 5x = 5 × 2 = 10
Height = 12x = 12 × 2 = 24 cm
Slant height = 13x = 13 × 2 = 26 cm
APPEARS IN
RELATED QUESTIONS
What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. [Use π = 3.14]
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assume that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm (Use it 𝜋 = 3.14)
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
The curved surface area of a cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
The area of the base of a conical solid is 38.5 cm2 and its volume is 154 cm3. Find the curved surface area of the solid.
A vessel, in the form of an inverted cone, is filled with water to the brim. Its height is 32 cm and diameter of the base is 25.2 cm. Six equal solid cones are dropped in it, so that they are fully submerged. As a result, one-fourth of water in the original cone overflows. What is the volume of each of the solid cones submerged?
A solid metal sphere is cut through its center into 2 equal parts. If the diameter of the sphere is `3 1/2 cm`, find the total surface area of each part correct to two decimal places.
The internal and external diameter of a hollow hemispherical vessel are 21 cm and 28 cm respectively. Find :
- internal curved surface area,
- external curved surface area,
- total surface area,
- volume of material of the vessel.
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. Find the radius of the base of each smaller cone, if height of each is 108 cm
A cone of height 15 cm and diameter 7 cm is mounted on a hemisphere of same diameter. Determine the volume of the solid thus formed.
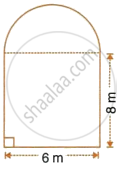
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m2.
Volume of a cone is 1232 cm3 and its height is 24 cm. Find the surface area of the cone. `( π = 22/7)`
Total surface area of a cone is 616 sq.cm. If the slant height of the cone is three times the radius of its base, find its slant height.
Find the height of the cone whose base radius is 5 cm and volume is 75π cm3.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
A metallic cylinder has a radius of 3 cm and a height of 5 cm. It is made of metal A. To reduce its weight, a conical hole is drilled in the cylinder, as shown and it is completely filled with a lighter metal B. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of the metal A to the volume of metal B in the solid.
A right-angled triangle PQR where ∠Q = 90° is rotated about QR and PQ. If QR = 16 cm and PR = 20 cm, compare the curved surface areas of the right circular cones so formed by the triangle
