Advertisements
Advertisements
Question
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm, each bullet being 4 cm in diameter?
Solution
In the given problem, we have a lead cube which is remolded into small spherical bullets.
Here, edge of the cube (s) = 44 cm
Diameter of the small spherical bullets (d) = 4 cm
Now, let us take the number of small bullets be x
So, the total volume of x spherical bullets is equal to the volume of the lead cube.
Therefore, we get,
Volume of the x bullets = volume of the cube
`x(4/3)pi (d/2)^3 = 8^3`
`x(4/3)(22/7)(4/2)^3 = (44)^3`
`x(4/3)(22/7)(2)^3 = 85184`
`x = ((85184)(3)(7))/((22)(4)(8))`
x =2541
Therefore, 2541 small bullets can be made from the given lead cube.
APPEARS IN
RELATED QUESTIONS
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per 100 cm2.
`["Assume "pi=22/7]`
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the
ratio of their surface areas.
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the adjoining figure. The tunnel is 80 m long.
Calculate:
- its volume,
- the surface area of the tunnel (excluding the floor) and
- its floor area.

A cylindrical rod whose height is 8 times of its radius is melted and recast into spherical balls of same radius. The number of balls will be
If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is
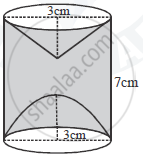
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
If the radius of a solid hemisphere is 5 cm, then find its curved surface area and total surface area. ( π = 3.14 )
A solid, consisting of a right circular cone standing on a hemisphere, is placed upright, in a right circular cylinder, full of water and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of the hemisphere is 2 cm and the height of the cone is 4 cm. Give your answer to the nearest cubic centimetre.
The cylinder of radius 12 cm have filled the 20 cm with water. One piece of iron drop in the stands of water goes up 6.75 cm. Find the radius of sphere piece.
The radius of a sphere increases by 25%. Find the percentage increase in its surface area
