Advertisements
Advertisements
प्रश्न
The volume of a sphere is 38808 cm3; find its diameter and the surface area.
उत्तर
Volume of the sphere = 38808 cm3
Let radius of sphere = r
∴ `4/3pir^3 = 38808 `
`=> 4/3 xx 22/7 xx r^3 = 38808`
`=> r^3 = (38808 xx 7 xx 3)/(4 xx 22) = 9261`
`=>` r = 21 cm
∴ Diameter = 2r
= 21 × 2 cm
= 42 cm
Surface area = 4πr2
= `4 xx 22/7 xx 21 xx 21`
= 5544 cm2
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of radius 5.6 cm.
`["Assume "pi=22/7]`
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of
painting it at the rate of Rs. 2 per sq. m.
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r cm.
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
The surface area of a sphere of radius 5 cm is five times the area of the curved surface of a cone of radius 4 cm. Find the height of the cone.
The total surface area of a hemisphere of radius r is
If a sphere is inscribed in a cube, then the ratio of the volume of the sphere to the volume of the cube is
Find the surface area and volume of sphere of the following radius. (π = 3.14)
4 cm
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
3.5 cm
Find the radius of a sphere whose surface area is equal to the area of the circle of diameter 2.8 cm
Find the radius of the sphere whose surface area is equal to its volume .
A solid metallic cylinder has a radius of 2 cm and is 45 cm tall. Find the number of metallic spheres of diameter 6 cm that can be made by recasting this cylinder .
The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate: the number of cones recasted [π = 3.14]
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
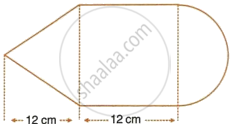
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
A solid, consisting of a right circular cone standing on a hemisphere, is placed upright, in a right circular cylinder, full of water and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of the hemisphere is 2 cm and the height of the cone is 4 cm. Give your answer to the nearest cubic centimetre.
There is surface area and volume of a sphere equal, find the radius of sphere.
The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. The ratios of the surface areas of the balloon in the two cases is ______.
A solid sphere is cut into two identical hemispheres.
Statement 1: The total volume of two hemispheres is equal to the volume of the original sphere.
Statement 2: The total surface area of two hemispheres together is equal to the surface area of the original sphere.
Which of the following is valid?
