Advertisements
Advertisements
प्रश्न
A heap of wheat is in the form of a cone of diameter 16.8 m and height 3.5 m. Find its volume. How much cloth is required to just cover the heap?
उत्तर
Diameter of the cone = 16.8 m
Therefore, radius (r) = 8.4 m
Height (h) = 3.5 m
i. Volume of heap of wheat = `1/3pir^2h`
= `1/3 xx 22/7 xx (8.4)^2 xx 3.5`
= `1/3 xx 22/7 xx 8.4 xx 8.4 xx 3.5`
= 258.72 m3
ii. Slant height (l) = `sqrt(r^2 + h^2)`
`sqrt((8.4)^2 + (3.5)^2)`
= `sqrt(70.56 + 12.25)`
= `sqrt(82.81)`
= 9.1 m
Therefore, cloth required or curved surface area = πrℓ
= `22/7 xx 8.4 xx 9.1`
= 240.24 m2
APPEARS IN
संबंधित प्रश्न
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
`["Assume "pi=22/7]`
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find
- radius of the base and
- total surface area of the cone.
`["Assume "pi =22/7]`
The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface.
The radius of a cone is 7 cm and area of curved surface is 176 `cm^2`. Find the slant height.
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find the radius of the base and total surface area of the cone.
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m
wide to make the required tent.
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8:5, show that the radius of each is to the height of each as 3:4.
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
The circumference of the base of a 12 m high conical tent is 66 m. Find the volume of the air contained in it.
The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2.
Calculate:
- its radius in cm.
- its volume in cm3. [Take π = 3.14].
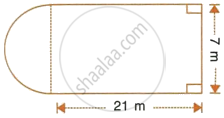
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
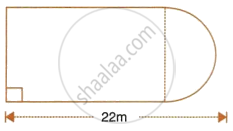
In the following diagram a rectangular platform with a semi-circular end on one side is 22 metres long from one end to the other end. If the length of the half circumference is 11 metres, find the cost of constructing the platform, 1.5 metres high at the rate of Rs. 4 per cubic metres.
Find the radius of the circular base of the cone , if its volume is 154 cm3 and the perpendicular height is 12 cm
Find the curved surface area of a cone whose height is 8 cm and base diameter is 12 cm .
Find the height of the cone whose base radius is 5 cm and volume is 75π cm3.
The curved surface area of a right circular cone of radius 11.3 cm is 710 cm2. What is the slant height of the cone ?
The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm3. What is its radius? What is its slant height? (Take π = 3.14)
