Advertisements
Advertisements
प्रश्न
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹ 210 per 100 m2.
`["Assume "pi=22/7]`
उत्तर
Slant height (l) of conical tomb = 25 m
Base radius (r) of tomb = `14/2` = 7 m
Curved surface area of conical tomb = πrl
=`(22/7 xx 7 xx 25) m^2`
= 550 m2
Cost of white-washing 100 m2 area = ₹ 210
Cost of white-washing 550 m2 area = `₹((210xx550)/100)`
= ₹ 1155
Therefore, it will cost ₹ 1155 while white-washing such a conical tomb.
APPEARS IN
संबंधित प्रश्न
If the radius of the base of a cone is halved, keeping the height same, what is the ratio of the volume of the reduced cone to that of the original cone?
A solid metal sphere is cut through its center into 2 equal parts. If the diameter of the sphere is `3 1/2 cm`, find the total surface area of each part correct to two decimal places.
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
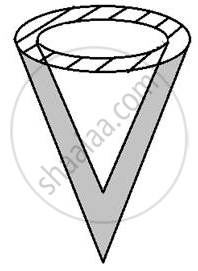
A buoy is made in the form of hemisphere surmounted by a right cone whose circular base coincides with the plane surface of hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-third of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
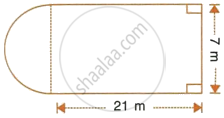
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
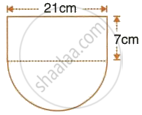
The given figure shows the cross section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
Surface area of a cone is 188.4 sq.cm and its slant height is 10 cm. Find its perpendicular height ( π= 3.14)
Total surface area of a cone is 616 sq.cm. If the slant height of the cone is three times the radius of its base, find its slant height.
Water flows at the rate of 10 m per minute through a cylindrical pipe 5 mm of diameter. How much time would it take to fill a conical vessel whose diameter at he surface is 40 cm and depth is 24 cm?
The ratio of the radii of two right circular cones of the same height is 1 : 3. Find the ratio of their curved surface area when the height cone is 3 times the radius of the smaller cone.
