Advertisements
Advertisements
प्रश्न
A vessel, in the form of an inverted cone, is filled with water to the brim. Its height is 32 cm and diameter of the base is 25.2 cm. Six equal solid cones are dropped in it, so that they are fully submerged. As a result, one-fourth of water in the original cone overflows. What is the volume of each of the solid cones submerged?
उत्तर
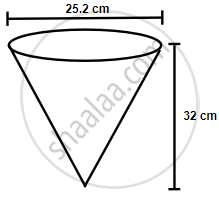
Volume of vessel = Volume of water = `1/3pir^2h`
Diameter = 25.2 cm,
Therefore radius = 12.6 cm
Height = 32 cm
Volume of water in the vessel = `1/3pir^2h`
= `1/3 xx 22/7 xx 12.6 xx 12.6 xx 32`
= 5322.24 cm3
On submerging six equal solid cones into it, one-fourth of the water overflows.
Therefore, volume of the equal solid cones submerged
= Volume of water that overflows
= `1/4 xx 5322.24`
= 1330.56 cm3
Now, volume of each cone submerged
= `1330.56/6`
= 221.76 cm3
APPEARS IN
संबंधित प्रश्न
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
`["Assume "pi=22/7]`
A joker’s cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
`["Assume "pi=22/7]`
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone.
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8:5, show that the radius of each is to the height of each as 3:4.
Find the volume of a right circular cone with:
radius 6 cm, height 7 cm.
Find the volume of a right circular cone with:
radius 3.5 cm, height 12 cm
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use 𝜋 = 3.14).
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilo litres?
The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
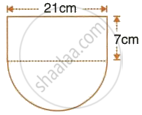
The given figure shows the cross section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
A solid, consisting of a right circular cone standing one a hemisphere, is placed upright in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of
the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimeter.
Find the curved surface area of a cone whose height is 8 cm and base diameter is 12 cm .
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: height of the tent.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg
The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm3. What is its radius? What is its slant height? (Take π = 3.14)
A metallic cylinder has a radius of 3 cm and a height of 5 cm. It is made of metal A. To reduce its weight, a conical hole is drilled in the cylinder, as shown and it is completely filled with a lighter metal B. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of the metal A to the volume of metal B in the solid.
