Advertisements
Advertisements
प्रश्न
A vessel, in the form of an inverted cone, is filled with water to the brim. Its height is 32 cm and diameter of the base is 25.2 cm. Six equal solid cones are dropped in it, so that they are fully submerged. As a result, one-fourth of water in the original cone overflows. What is the volume of each of the solid cones submerged?
उत्तर
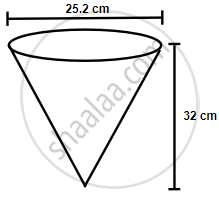
Volume of vessel = Volume of water = `1/3pir^2h`
Diameter = 25.2 cm,
Therefore radius = 12.6 cm
Height = 32 cm
Volume of water in the vessel = `1/3pir^2h`
= `1/3 xx 22/7 xx 12.6 xx 12.6 xx 32`
= 5322.24 cm3
On submerging six equal solid cones into it, one-fourth of the water overflows.
Therefore, volume of the equal solid cones submerged
= Volume of water that overflows
= `1/4 xx 5322.24`
= 1330.56 cm3
Now, volume of each cone submerged
= `1330.56/6`
= 221.76 cm3
APPEARS IN
संबंधित प्रश्न
What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. [Use π = 3.14]
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹ 210 per 100 m2.
`["Assume "pi=22/7]`
The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. This common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.

Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
The radius and slant height of a cone are In the ratio of 4 : 7. If its curved surface area is 792 cm2, find its radius. (Use it 𝜋 = 22/7).
There are two cones. The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
Find the volume of a right circular cone with:
radius 3.5 cm, height 12 cm
If the radius of the base of a cone is halved, keeping the height same, what is the ratio of the volume of the reduced cone to that of the original cone?
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
Find what length of canvas, 1.5 m in width, is required to make a conical tent 48 m in diameter and 7 m in height. Given that 10% of the canvas is used in folds and stitchings. Also, find the cost of the canvas at the rate of Rs. 24 per metre.
The area of the base of a conical solid is 38.5 cm2 and its volume is 154 cm3. Find the curved surface area of the solid.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the:
- radius of the floor,
- height of the tent,
- length of the canvas required to cover this conical tent if its width is 2 m.
The internal and external diameter of a hollow hemispherical vessel are 21 cm and 28 cm respectively. Find :
- internal curved surface area,
- external curved surface area,
- total surface area,
- volume of material of the vessel.
The curved surface area of a cone is 2200 sq.cm and its slant height is 50 cm. Find the total surface area of cone. `(π = 22/7)`
Find the radius of the circular base of the cone , if its volume is 154 cm3 and the perpendicular height is 12 cm
The curved surface area of a right circular cone of radius 11.3 cm is 710 cm2. What is the slant height of the cone ?
A sphere and a cone have the same radii. If their volumes are also equal, prove that the height of the cone is twice its radius.
The ratio of the base area and the curved surface of a conical tent is 40: 41. If the height is 18 m, Find the air capacity of the tent in terms of n.
The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. How many students can sit in the tent if a student, on an average, occupies `5/7` m2 on the ground?
