Advertisements
Advertisements
प्रश्न
The area of the base of a conical solid is 38.5 cm2 and its volume is 154 cm3. Find the curved surface area of the solid.
उत्तर
Area of the base, πr2 = 38.5 cm2
Volume of the solid, V = 154 cm3
Curved surface area of the solid = πr2h
Volume, V `= 1/3 pir^2h`
`=> 154 = 1/3 pir^2h`
`=> h = (154 xx 3)/(pir^2)`
`=> h = (154 xx 3)/38.5`
= 12 cm
Area = 38.5
πr2 = 38.5
`=> r^2 = 38.5/3.14`
`=> r = sqrt(38.5/3.14)`
= 3.5
Curved surface area of solid = πrl
= `pirsqrt(r^2 + h^2)`
= `22/7 xx 3.5 xx sqrt(3.5^2 + 12^2)`
= `22/7 xx 3.5 xx 12.5`
= 137.5 cm2
APPEARS IN
संबंधित प्रश्न
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
A Joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
The circumference of the base of a 10 m height conical tent is 44 metres. Calculate the length of canvas used in making the tent if width of canvas is 2 m. (Use it 𝜋= 22/7).
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assume that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm (Use it 𝜋 = 3.14)
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use 𝜋 = 3.14).
A right angled triangle of which the sides containing he right angle are 6.3 cm and lo cm in length, is made to turn round on the longer side. Find the volume of the solid, thus generated. Also, find its curved surface area.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilo litres?
The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2.
Calculate:
- its radius in cm.
- its volume in cm3. [Take π = 3.14].
A solid sphere and a solid hemi-sphere have the same total surface area. Find the ratio between their volumes.
The radii of the bases of two solid right circular cones of same height are r1 and r2 respectively. The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms r1, r2 and R.
A solid metallic hemisphere of diameter 28 cm is melted and recast into a number of identical solid cones, each of diameter 14 cm and height 8 cm. Find the number of cones so formed.
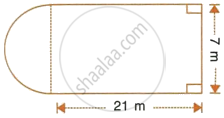
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
Find the height of the cone whose base radius is 5 cm and volume is 75π cm3.
A buoy is made in the form of a hemisphere surmounted by a right circular cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 m and its volume is two-third the volume of hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two decimal places.
