Advertisements
Advertisements
प्रश्न
A spherical shell of lead, whose external and internal diameters are 24 cm and 18 cm, is melted and recast into a right circular cylinder 37 cm high. Find the diameter of the base of the cylinder.
उत्तर
External diameter of the shell = 24 cm
External radius of the shell = 12 cm
Internal diameter of the shell = 18 cm
Internal radius of the shell = 9 cm
Volume of the
`"shell" = 4/3pi (12^3 -9^3) =4/3pi(1728 - 729)=4/3pixx(999)=4pi xx (333) "cm"^3`
Height of cylinder = 37 cm
Let radius of cylinder be r cm.
Volume of cylinder =`pir^2h = 37pir^2 "cm"^3`
Volume of the shell = Volume of cylinder
Or, 4π ×(333)= 37πr2
`⇒ r^2=(4xx333)/37 = 4xx9`
`rArr r =sqrt(4xx9)=sqrt(36) = 6 "cm"`
So, diameter of the base of the cylinder = 2r = 12 cm.
APPEARS IN
संबंधित प्रश्न
25 circular plates each of radius 10.5cm and thickness 1.6cm are placed one above the other to form a solid circular cylinder. Find the curved surface area and volume of cylinder so formed?
A well with inner radius 4m is dug 14m deep earth taken out of it has been spread evenly all around a width of 3m it to form an embankment. Find the height of the embankment?
A bucket made up of a metal sheet is in form of a frustum of cone of height 16cm with diameters of its lower and upper ends as 16cm and 40cm. find the volume of bucket. Also find cost of bucket if the cost of metal sheet used is Rs 20 per 100 cm2
12 spheres of the same size are made from melting a solid cylinder of 16 cm diameter and 2 cm height. The diameter of each sphere is
The radii of internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm, respectively. It is melted and recast into a solid cylinder of diameter 14 cm. Find the height of the cylinder.
The boundary of the shaded region in the given diagram consists of three semicircular areas, the smaller ones being equal and it’s diameter 5 cm, if the diameter of the larger one is 10 cm,
calculate:
(i) The length of the boundary,
(ii) The area of the shaded region. (Take π = 3.14)

A wall 24 m long, 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm × 16 cm × 10 cm. If the mortar occupies `1/10` th of the volume of the wall, then find the number of bricks used in constructing the wall.
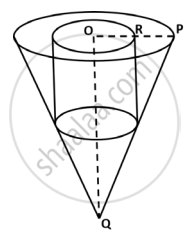
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)
Find the volume of a solid hemisphere whose total surface area is 462 sq.m.
A student was asked to make a model shaped like a cylinder with two cones attached to its ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its total length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model.
