Advertisements
Advertisements
प्रश्न
A wall 24 m long, 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm × 16 cm × 10 cm. If the mortar occupies `1/10` th of the volume of the wall, then find the number of bricks used in constructing the wall.
उत्तर
Given that, a wall is constructed with the help of bricks and mortar.
∴ Number of bricks = `(("Volume of wall") - (1/10 "th volume of wall"))/"Volume of a brick"` ...(i)
Also, given that
Length of a wall (l) = 24 m,
Thickness of a wall (b) = 0.4 m,
Height of a wall (h) = 6 m
So, volume of a wall constructed with the bricks = l × b × h
= 24 × 0.4 × 6
= `(24 xx 4 xx 6)/10 "m"^3`
Now, `1/10`th volume of a wall
= `1/10 xx (24 xx 4 xx 6)/10`
= `(24 xx 4 xx 6)/10^2 "m"^3`
And length of a brick (l1) = 25 cm = `25/100 "m"`
Breadth of a brick (b1) = 16 cm = `16/100 "m"`
Height of a brick (h1) = 10 cm = `10/100 "m"`
So, volume of a brick = l1 × b1 × h1
= `25/100 xx 16/100 xx 10/100`
= `(25 xx 16)/10^5 "m"^3`
From equation (i),
Number of bricks = `(((24 xx 4 xx 6)/10 - (24 xx 4 xx 6)/100))/(((25 xx 16)/10^5)`
= `(24 xx 4 xx 6)/100 xx 9 xx 10^5/(25 xx 16)`
= `(24 xx 4 xx 6 xx 9 xx 1000)/(25 xx 16)`
= 24 × 6 × 9 × 10
= 12960
Hence, the required number of bricks used in constructing the wall is 12960.
APPEARS IN
संबंधित प्रश्न
A rectangular tank 15m long and 11m broad is required to receive entire liquid contents from a full cylindrical tank of internal diameter 21m and length 5m. Find least height of tank that will serve purpose .
The diameter of a metallic sphere is equal to 9cm. it is melted and drawn into a long wire of diameter 2mm having uniform cross-section. Find the length of the wire?
A vessel in the shape of cuboid ontains some water. If these identical spheres are immersed in the water, the level of water is increased by 2cm. if the area of base of cuboid is 160cm2 and its height 12cm, determine radius of any of spheres?
A solid metallic sphere of radius 8 cm is melted and recast into spherical balls each of radius 2 cm. Find the number of spherical balls obtained.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is ______.
The boundary of the shaded region in the given diagram consists of three semicircular areas, the smaller ones being equal and it’s diameter 5 cm, if the diameter of the larger one is 10 cm,
calculate:
(i) The length of the boundary,
(ii) The area of the shaded region. (Take π = 3.14)

The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
A surahi is the combination of ______.
Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube. Find the edge of the cube so formed.
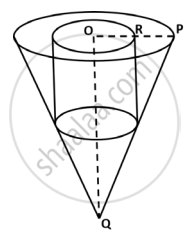
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)