Advertisements
Advertisements
प्रश्न
A vessel in the shape of cuboid ontains some water. If these identical spheres are immersed in the water, the level of water is increased by 2cm. if the area of base of cuboid is 160cm2 and its height 12cm, determine radius of any of spheres?
उत्तर
Given that area of cuboid = 160cm2
Level of water increased in vessel = 2cm
Volume of a vessel = 160 x 2cm3 .......(1)
Volume of each sphere =`4/3pir^3cm^3`
Total volume of 3 spheres `=3xx4/3pir^3cm^3` ...........(2)
Equating (1) and (2) ∵Volumes are equal V1 = V2
`160xx2=3xx4/3pir^3`
`r^3=(160xx2)/(3xx4/3pi)
`r^3=320/(4pi)`
r = 2.94cm
∴ Radius of sphere = 2.94cm
APPEARS IN
संबंधित प्रश्न
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
Find the volume of the largest right circular cone that can be cut out of a cube where edgeis 9cm?
The surface area of a solid metallic sphere is 616 cm2. It is melted and recast into a cone of height 28 cm. Find the diameter of the base of the cone so formed (Use it =`22/7`)
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. (Use π = 22/7).
A solid right circular cone of height 60 cm and radius 30 cm is dropped in a right circular cylinder full of water, of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres.
Choose the correct answer of the following question:
If the radius of a sphere becomes 3 times, then its volume will become
A mason constructs a wall of dimensions (270 cm × 300 cm × 350 cm) with bricks, each of size (22.5 cm × 11.25 cm × 8.75 cm) and it is assumed that `1/8` space is covered by the mortar. Number of bricks used to construct the wall is ______.
The circumference of the edge of hemispherical bowl is 132 cm. When π is taken as `22/7`, the capacity of bowl in cm³ is ______.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
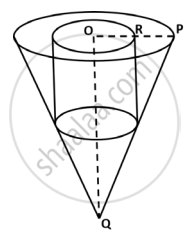
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)