Advertisements
Advertisements
प्रश्न
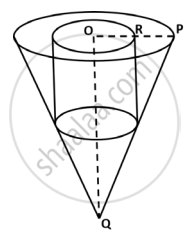
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)
उत्तर
Cons -
OP (r) = 7 cm
OQ (h) = 12 cm
Cylinders -
r' = `7/2` cm
h' = `12/2` = 6 cm
Volume = Volume of Cone - Volume of cylinder
`= 1/3 pi"r"^2"h" - pi"r'"^2 "h'"^2`
`= 1/3 xx pi xx 7 xx 7 xx 12 - pi xx 7/2 xx 7/2 xx 6`
`= pi xx 7 xx 7 {1/(cancel3) xx cancel(12)^4 - 1/cancel(2) xx 1/2 xx (cancel(6)^3}`
`= 22/7 xx 7 xx 7 xx {4 - 1.5}`
= 22 × 7 × 2.5
= 385 cm3
APPEARS IN
संबंधित प्रश्न
2.2 Cubic dm of grass is to be drawn into a cylinder wire 0.25cm in diameter. Find the length of wire?
Water in a canal 1.5m wide and 6m deep is flowering with a speed of 10km/ hr. how much area will it irrigate in 30 minutes if 8cm of standing water is desired?
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block.
A toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21 cm and its volume is `2/3` of the volume of hemisphere, calculate the height of the cone and the surface area of the toy.
`(use pi = 22/7)`
A hemispherical depression is cut out from one face of a cubical block of side 7 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Find the surface area of the remaining solid. [Use π = \[\frac{22}{7}\]]
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid. [Use`pi22/7`]
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the volume of water
- displaced out of the cylinder
- left in the cylinder.
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimensions 66 cm, 42 cm and 21 cm.
A wall 24 m long, 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm × 16 cm × 10 cm. If the mortar occupies `1/10` th of the volume of the wall, then find the number of bricks used in constructing the wall.
