Advertisements
Advertisements
प्रश्न
A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block.
उत्तर
We have to find the remaining volume and surface area of a cubical box when a hemisphere is cut out from it.
Edge length of cube(a) = 21cm
Radius of hemisphere(r) = 10.5 cm
Therefore volume of the remaining block,
= Volume of box - Volume of hemisphere
So,
`=(a)^3-2/3pir^3`
`=(21)^3-2/3(22/7)(21/2)^3`
=(9261 - 2425.5) cm3
= 6835.5 cm3
So, remaining surface area of the box,
=surface area of box - Area of base of hemisphere +Curved surface area of hemsphere
Therefore,
`=6(a)^2-pir^2+2pir^2`
= 6(a)2 + πr2
Put the values to get the remaining surface area of the box,
`=[6(441)+22/7(21/2)^2]cm^2`
= 2992.5 cm2
APPEARS IN
संबंधित प्रश्न
Find the volume of the largest right circular cone that can be cut out of a cube where edgeis 9cm?
A vessel in the shape of cuboid ontains some water. If these identical spheres are immersed in the water, the level of water is increased by 2cm. if the area of base of cuboid is 160cm2 and its height 12cm, determine radius of any of spheres?
The volume of a wall, 5 times as high as it is broad and 8 times as long as it is high, is 128 m3. The breadth of the wall is
How many bags of grain can be stored in a cuboidal granary (8 m × 6 m × 3 m), if each bag occupies a space of 0.64 m3?
A hollow metallic sphere with external diameter 8 cm and internal diameter 4 cm is melted and moulded into a cone of base radius 8 cm. The height of the cone is
The circumference of the edge of hemispherical bowl is 132 cm. When π is taken as `22/7`, the capacity of bowl in cm³ is ______.
A surahi is the combination of ______.
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder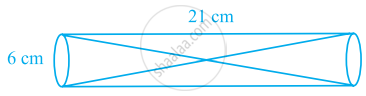
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
A solid is in the shape of a right-circular cone surmounted on a hemisphere, the radius of each of them being 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.
