Advertisements
Advertisements
Question
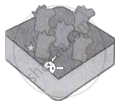
A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block.
Solution
We have to find the remaining volume and surface area of a cubical box when a hemisphere is cut out from it.
Edge length of cube(a) = 21cm
Radius of hemisphere(r) = 10.5 cm
Therefore volume of the remaining block,
= Volume of box - Volume of hemisphere
So,
`=(a)^3-2/3pir^3`
`=(21)^3-2/3(22/7)(21/2)^3`
=(9261 - 2425.5) cm3
= 6835.5 cm3
So, remaining surface area of the box,
=surface area of box - Area of base of hemisphere +Curved surface area of hemsphere
Therefore,
`=6(a)^2-pir^2+2pir^2`
= 6(a)2 + πr2
Put the values to get the remaining surface area of the box,
`=[6(441)+22/7(21/2)^2]cm^2`
= 2992.5 cm2
APPEARS IN
RELATED QUESTIONS
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). Use [π = `22/7`]

A solid iron pole having cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that the mass of 1 cm3of iron is 8 gm.
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them being 3.5 cm and the total height of the solid is 9.5 cm. Find the volume of the solid.
How many bricks, each measuring (25 cm × 11.25 cm × 6 cm), will be required to construct a wall (8 m × 6 m × 22.5 cm)?
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii?
A solid rectangular block of dimensions 4.4 m, 2.6 m and 1 m is cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube. Find the edge of the cube so formed.
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder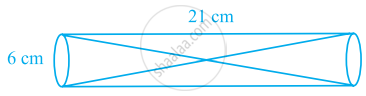
A wall 24 m long, 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm × 16 cm × 10 cm. If the mortar occupies `1/10` th of the volume of the wall, then find the number of bricks used in constructing the wall.
Read the following passage and answer the questions given below.
|
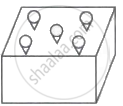
A solid cuboidal toy is made of wood. It has five cone-shaped cavities to hold toy carrots. The dimensions of the toy cuboid are – 10 cm × 10 cm × 8 cm. Each cone carved out – Radius = 2.1 cm and Height = 6 cm
|
- Find the volume of wood carved out to make five conical cavities.
- Find the volume of the wood in the final product.