Advertisements
Advertisements
Question
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii?
Solution
Let the radii of the two cylinders be r and R; and height be h and we have,
`"h"/"H" = 1/2` ...........(i)
Volume of the first cylinder = Volume of the second sphere
⇒ πr2 H = πR2 H
`⇒ "h"/"H" = "R"^2/"r"^2`
`=> 1/2 = "R"^2/"r"^2`
`=> "r"^2/"R"^2 = 1/2`
`=> ("r"/"R")^2=1/2`
`=>"r"/"R" = sqrt(2/1)`
`∴ "r" : "R" =sqrt(2:1)`
So, the ratio of their radii is `sqrt(2)` : 1.
APPEARS IN
RELATED QUESTIONS
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball is dropped into the tube and the level of the water is raised by 6.75cm.Find the radius of the ball .
The volume of a hemisphere is 2425`1/2cm^3`cm. Find its curved surface area?
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block.
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. (Use π = 22/7).
The height of a cone is 20 cm. A small cone is cut off from the top by a plane parallel to the base. If its volume be 1/125 of the volume of the original cone, determine at what height above the base the section is made.
How many lead balls, each of radius 1 cm, can be made from a sphere of radius 8 cm?
A copper sphere of diameter 18 cm is drawn into a wire of diameter 4 mm. Find the length of the wire.
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder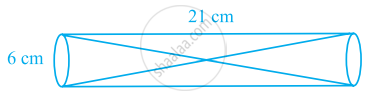
The sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm and the length of its diagonal is `2sqrt(3)` cm. The total surface area of the cuboid is ______.
