Advertisements
Advertisements
प्रश्न
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
उत्तर
Volume of water in tank = Volume of cuboidal tank up to a height of 5 m
According to the question,
For cuboidal tank
Length, l = 11 m
Breadth, b = 6 m
Height, h = 5 m
We know that the equation to find the volume of the tank,
Volume of tank = lbh, where, l, b and h are the length, breadth and height of tank respectively
Volume of water = 11(6)(5) = 330 m3
We also know that,
Base radius of cylindrical tank, r = 3.5 m
Let the height till which the cylindrical tank is filled = h m
Hence, using the formula,
Volume of a cylinder = πr2h, where r is base radius and h is the height of cylinder
Volume of water in cylindrical tank = π(3.5)2h
330 m3 = `22/7 xx 3.5 xx 3.5 xx "h"`
330 m3 = h × 38.5
h = 8.57 m
Hence, the height till which the cylindrical tank is filled = 8.57 m
APPEARS IN
संबंधित प्रश्न
A hollow sphere of internal and external radii 2cm and 4cm is melted into a cone of basse radius 4cm. find the height and slant height of the cone______?
Metal spheres each of radius 2cm are packed into a rectangular box of internal dimension 16cm x 8cm x 8cm when 16 spheres are packed the box is filled with preservative liquid. Find volume of this liquid?
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the hemisphere is immersed in the tub. If the radius of the hemi-sphere is 3.5 cm and height of the cone outside the hemisphere is 5 cm, find the volume of the water left in the tub (Take π = 22/7)
The height of a cone is 20 cm. A small cone is cut off from the top by a plane parallel to the base. If its volume be 1/125 of the volume of the original cone, determine at what height above the base the section is made.
150 spherical marbles, each of diameter 1.4 cm, are dropped in a cylindrical vessel of diameter 7 cm containing some water, which are completely immersed in water. Find the rise in the level of water in the vessel.
The diameter of a sphere is 14 cm. Its volume is
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii?
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
Water flows through a cylindrical pipe, whose inner radius is 1 cm, at the rate of 80 cm/sec in an empty cylindrical tank, the radius of whose base is 40 cm. What is the rise of water level in tank in half an hour?
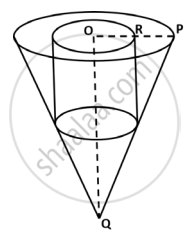
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)