Advertisements
Advertisements
प्रश्न
The height of a cone is 20 cm. A small cone is cut off from the top by a plane parallel to the base. If its volume be 1/125 of the volume of the original cone, determine at what height above the base the section is made.
उत्तर
We have the following situation as shown in the figure
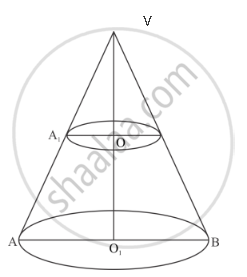
Let VAB be a cone of height h1 = VO1 =20cm. Then from the symmetric triangles VO 1A and VOA1, we have
`(VO_1)/(VO)=(O_1A)/(OA_1)`
⇒`20/(VO)=(O_1A)/(OA_1)`
It is given that, volume of the cone VA1O is`1/125`times the volume of the cone VAB. Hence, we have
`1/3piOA_1^2xxVO=1/125xx1/3piO_1A^2xx20`
⇒`((OA_1)/(O_1A))^2xxVO=4/25`
⇒`((VO)/20)^2xxVO=4/25`
⇒`VO^3=(400xx4)/25`
⇒ VO3 = 16 x 4
⇒ VO = 4
Hence, the height at which the section is made is 20 − 4 = 16 cm.
APPEARS IN
संबंधित प्रश्न
The largest sphere is to be curved out of a right circular of radius 7cm and height 14cm. find volume of sphere?
A well with inner radius 4m is dug 14m deep earth taken out of it has been spread evenly all around a width of 3m it to form an embankment. Find the height of the embankment?
Water in a canal 1.5m wide and 6m deep is flowering with a speed of 10km/ hr. how much area will it irrigate in 30 minutes if 8cm of standing water is desired?
A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block.
A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, then find the height of the toy.
From a solid cylinder of height 14 cm and base diameter 7 cm, two equal conical holes each of radius 2.1 cm and height 4 cm are cut off. Find the volume of the remaining solid.
A copper rod of diameter 2 cm and length 10 cm is drawn into a wire of uniform thickness and length 10 m. Find the thickness of the wire.
The diameter of a copper sphere is 18 cm. It is melted and drawn into a long wire of uniform cross-section. If the length of the wire is 108 m, find its diameter.
Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, are melted and recast into a single large cube. Find the edge of the new cube formed.
In the equilateral Δ ABC of side 14 cm, side BC is the diameter of a semicircle as shown in the figure below. Find the area of the shaded region. (Take π = 22/7 and √3 = 1.732)